Abstract
A belief shared by Albert Einstein and by Sir Arthur Stanley Eddington involved the probable existence of some unrecognized law of nature that prevents unrestricted gravitational collapse. The present article builds on this belief by making the reasonable assumption that Nature imposes an absolute limit on the density of mass. This premise of an ultimate density state becomes the key to resolving the mystery of why the overwhelming number of neutron stars have the same total mass value. The mystery involves the long-standing question, Why is there this amazing over-representation of neutron bodies measuring 1.4 solar mass? It turns out these identically-massed bodies are the neutron stars that have acquired a critical-state surface and, so, have reached their final (and identical) evolutionary state —and are recognized as End-State neutron stars. Then, using conventional physics, the radius, volume, and density immediately follow. Finally, by incorporating the simple mass-annihilation mechanism from DSSU theory (currently the most advanced problem-free cosmology), it is revealed how the Terminal state is maintained —how, regardless of the mass quantity an End-State neutron star absorbs, its total mass of 1.4 solar mass never ever changes!
Keywords
Neutron Stars, End-State Neutron Star, Terminal Star, Ultimate Density, Mass Extinction, Mass Annihilation, Aether Deprivation, Black Hole Physics
1. Introduction
A remarkable development in recent years in our theoretical understanding of how the Universe works has led to the resolution of a variety of problems in cosmology and astrophysics. Highlights of these are available and are presented in a number of posted Press Releases
at CellularUniverse.org. The new insight provides scientists and philosophers with a key component of the ontological nature of the physical realm. All matter —all mass and energy particles, anything physical, without exception— absorbs and consumes a
universal medium in order to sustain its existence. It ‘feeds’ on what is best described as an all-permeating ethereal substrate. The very existence of matter depends on a continuous absorption/consumption of this sub-physical essence.
The present article makes use of this profound principle in order to determine Nature’s maximal mass density and to resolve a long-standing question on the maximum total mass that a non-rotating neutron star can have.
2. A Simple Choice, a Reasonable Assumption
A simple choice presents itself: Nature either has a maximal density state or it does not.
Most physicists, most researchers, have long embraced the latter view. They favored a limitless density whose mathematical representation is a singularity. Theirs is a radical assumption that underlies black hole physics.
What makes a reassessment of the choice so utterly effortless is the fact that conventional black hole theory is plagued by a number of paradoxes. They are conspicuous, they are irresolvable, they are embarrassing. Consider the following: If gravity is a form of energy, how is the gravitational energy of the black hole’s mass able to extend its reach through the event horizon, and beyond, and influence the external region? Why isn’t the energy of the gravitational field inside (inside the sphere defined by the event-horizon boundary) completely absorbed by the alleged singularity? Since gravity is an effect generated by mass, then, for the effect to manifest in the region between the black hole’s point-like mass and the event horizon, it would have to propagate much faster than the speed of light! Then there is the angular momentum paradox. How is it possible to claim (as physicists Charles Misner, Kip Thorne and John Wheeler have done) that black holes have the capacity for angular momentum? By definition, angular momentum requires a radius for the material that is present; while, also by definition, the radius of the matter of a singularity black-hole is infinitely small, effectively zero; hence, a paradox. Also worth citing is the obvious conundrum of packing a vast quantity of mass inside a speck of zero nominal volume.
These issues are all well-known, but little-discussed. And they are entirely avoidable.
It is simply a matter of recognizing that a singularity is purely a mathematical entity and not a real point-mass.
The solution is to adopt the perfectly reasonable assumption that Nature has an ultimate density.
Determining Nature’s limiting density entails a close look at gravitationally collapsed bodies, namely neutron stars.
3. Neutron Stars
3.1. Formation of Neutron Stars
When a sufficient quantity of mass becomes concentrated within a relatively small volume, a neutron star is formed. This can happen in a number of ways. Most spectacularly it happens as a result of the gravitational collapse of some significantly larger body; it happens catastrophically when the dense core, having exhausted its nuclear fuel, collapses and triggers a blazing supernova event. Astrophysicist Edward Harrison has described the final sequence in the process of stellar-core collapse as follows: "The central density and temperature continue to rise and eventually reach a point where the heavy elements in the core are crushed and broken down into helium. Finally, the helium dissolves into its constituent particles: protons, neutrons, and electrons. The electrons get squeezed into the protons, leaving neutrons as the dominant survivors in the collapsed core
| [8] | Harrison, E.R. (2003) Masks of the Universe, Changing Ideas on the Nature of the Cosmos (2nd ed. Cambridge University Press, Cambridge, UK, 2003). P187. |
[8]
." Formation also comes about as a result of the gravitational merger(s) of dense dwarf stars; or, it can occur through the gradual gravitational accretion of mass by a dwarf star (a White dwarf or even a burned-out none-radiating dwarf). Once a neutron star has formed, it is supported against further collapse by neutron-degeneracy pressure and repulsive nuclear forces. A minimal neutron star has a mass of about three-quarters the mass of our Sun. Progressively more massive bodies are supported by this combination of degeneracy pressure and nuclear forces. But there is a limit. It seems the neutron-degeneracy pressure is sufficient to hold up the structure only if the total mass does not exceed 2.2 solar masses (2.2
M⊙) and does not rotate excessively
This 2.2 mass figure gained credibility in 2018. As reported by Science Daily, “Astrophysicists set a new limit for the maximum mass of [spherical] neutron stars: It cannot exceed 2.16 [~2.2] solar masses.” Based on research by Professor Luciano Rezzolla (Theoretical Astrophysics at Goethe University Frankfurt) and his team, “With an accuracy of a few percent, the maximum mass of non-rotating neutron stars cannot exceed 2.16 solar masses
.”
Newly minted neutron stars, as shown in
Figure 1, can be divided into three broad categories:
1) Spherical neutron stars with negligible spin. This category encompasses neutron stars weighing less than about 2.2 M⊙.
2) Oblate-shaped neutron stars —oblate because of significant spin. This category encompasses the complete mass-range of neutron stars (extending to around 3.3 M⊙).
3) End-state neuron stars —always spherical regardless of the rate of rotation. This category holds the key to Nature’s maximal density state.
These three categories are useful for understanding the connection between subsequent evolution and the observational evidence —a connection that has long puzzled astronomers and theorists.
A clarification. As just noted, the category of “spherical low-spin” may be as massive as 2.2
M⊙. Does this not then conflict with the use (in
Figure 1) of a 1.4
M⊙ limit for end-state neutron stars?... No. In order to attain the 1.4
M⊙ limit, a pre-existing 2.2
M⊙-mass neutron star must acquire additional mass; while in the case of stellar-core collapse, kinetic pressure assists the basic gravitational pressure to overcome the neutron-degeneracy pressure (leaving in place an ultimate repulsive nuclear force). As noted in
Figure 1, it is the combination of
total mass and kinetic pressure that is important for collapse to the ultimate compact state of 1.4
M⊙.
Figure 1. Formation of neutron stars can occur as a result of (i) the collapse of a stellar core; (ii) the gradual accretion of mass by Dwarf stars; (iii) orbital mergers and direct collisions of compact bodies; (iv) a wide variety of accrual scenarios. Newly formed neutron stars can be classed as sub-maximal density (split further as low spin and high spin) and maximal density (end-state neutron stars). Once forged, these objects continue to be subject to mergers, collisions, and accretion. Empirical evidence suggests that the total mass of individual neutron stars may range from 0.7 M⊙ to about 3.3 M⊙.
The evolution and non-evolution of neutron stars (
Figure 2). As one would expect, all neutron stars undergo further mass acquisition through mergers, collisions, and/or gradual accretion. But there are notable distinctions between the categories. Members of the first two categories undergo a transformation; members of the third do not. Distinguishing the three categories are the following key anatomical characteristics:
i. The low spin type have mass limit of about 2.2 M⊙. If a member accrues enough mass causing it to exceed this limit, it will immediately transform (collapse) into an End-State neutron star. It becomes what is termed a Terminal star, a shorter term that is wholly synonymous with the longer ‘End-State neutron star.’ (The only alternative fate is for it to be absorbed by a preexisting Terminal star.)
ii. The high spin type have mass limit of about 3.3 M⊙. The triggering criterion, here, is a combination of spin rate and total mass. Sooner or later, this combination will result in the neutron star’s surface becoming critical. This means the surface immediately transforms to pure energy (a layer of photons and neutrinos), triggering the member to suddenly transition (collapse) into an End-State neutron star. Thus, it too becomes a Terminal star. (Again, the only alternative fate is for it to be absorbed by a preexisting Terminal star.)
iii. The End-State neutron stars never deviate from their characteristic 1.4
M⊙. Members, here, all weigh the same. Except for spin rates and polar-emission characteristics, they are carbon copies. Although the individual rate of rotation may differ drastically, amazingly, the structure always remains perfectly spherical
| [12] | Ranzan, C. (2021) Law of Physics 20th-Century Scientists Overlooked (Part 5): Centrifugal Effect Negation, Applied Physics Research Vol. 13, No. 2, pp. 13-34 (2021). https://doi.org/10.5539/apr.v13n2p13 |
[12]
.
Notice, there is no ‘black hole’ category. The density assumption precludes it. There can be no further contraction beyond what is shown in
Figure 2.
3.2. Mass Range of Neutron Stars
The empirical evidence indicates that individual neutron stars may range in total mass from about 0.70 M⊙ to over 3.3 M⊙. The following are some noteworthy examples:
1) The object associated with the supernova remnant HESS J1731-347 is believed to be the smallest neutron star ever detected. A careful reanalysis of this object by researchers at the University of Tübingen in Germany (in 2022) led them to conclude it is a neutron star around
0.77 times the mass of the sun and 20
kilometres in diameter
| [13] | Doroshenko, V.; Suleimanov, V.; Pühlhofer, G.; & Santangelo, A. (2022) "A strangely light neutron star within a supernova remnant". Nature Astronomy 6, pp. 1444-1451 (2022). https://doi.org/10.1038/s41550-022-01800-1 |
[13].
2) Back in 2010, the millisecond pulsar PSR J1614−2230, as measured by Paul Demorest and colleagues, weighed in at 1.97±0.04 M⊙. This was substantially higher than the previously most-massive neutron star PSR J1903+0327, which measured 1.67±0.02 M⊙. –Neutron Stars, Wikipedia (2025-4).
3) In 2018, the neutron star known as PSR J0348+0432 (another pulsar) was determined to have a total mass of
2.01 M⊙ and a radius of 12
kilometers.
| [11] | Rezzolla, L.; Most, E.R.; Weih, L.R. (2018) Using Gravitational-wave Observations and Quasi-universal Relations to Constrain the Maximum Mass of Neutron Stars. The Astrophysical Journal, Vol. 852(2): L25 (2018). https://doi.org/10.3847/2041-8213/aaa401 |
[11]
. Then in 2025, another group using an improved analysis of PSR J0348+0432 arrived at total mass of
1.8 M⊙ .
4) In 2021, a neutron star in the northern constellation Camelopardalis named PSR J0740+6620 was measured and found to be about
2.08 times as massive as the sun
.
5) In 2022, PSR J0952-0607 was deemed the most massive pulsar with
2.35±0.17 M⊙. According to the study’s coauthor Roger Romani, an astrophysicist at Stanford University, “That’s the heaviest well-measured neutron star that has been found to date
| [16] | Croswell, K. (2022-7-22) "The heaviest neutron star on record is 2.35 times the mass of the sun". Science News. Retrieved 2022-7-25. |
| [17] | Romani, R.W.; Kandel, D.; Filippenko, A.V.; Brink, T.G.; Zheng, W. (2022) "PSR J0952−0607: The Fastest and Heaviest Known Galactic Neutron Star". The Astrophysical Journal Letters, Vol. 934, (2): L17 (2022-7-11). https://doi.org/10.3847/2041-8213/ac8007 |
[16, 17]
.”
6) In 2024 a consortium of astronomers reported detecting a neutron star (an unnamed companion of the millisecond pulsar PSR J0514−4002E) whose mass was estimated to be between
2.09 to
2.71 M⊙. The unexpected high mass of the companion, they proposed, was the result of a merger between two earlier neutron stars
| [18] | Barr, E.D.; Dutta, A.; Freire, P.C.; Cadelano, M.; Gautam, T.; Kramer, M.;... & Possenti, A. (2024) "A pulsar in a binary with a compact object in the mass gap between neutron stars and black holes". Science, 383(6680), (2024) pp. 275-279. https://www.science.org/doi/abs/10.1126/science.adg3005 |
[18]
.
7) A 3.3
M⊙ neutron star in a binary system with a companion giant star (a rapidly rotating giant) may well be the most massive neutron star ever discovered. “[Observational] constraints on the giant’s mass and radius imply that the unseen companion is 3.3
−0.7+2.8 solar masses, indicating that it is a noninteracting low-mass black hole or an unexpectedly massive neutron star
| [19] | Thompson, T.A.; Kochanek, C.S.; Stanek, K.Z.; Badenes, C.; [...], and Covey, K. (2019) "A noninteracting low-mass black hole–giant star binary system". Science, Vol. 366, Issue 6465, pp. 637-640 (2019). https://www.science.org/doi/10.1126/science.aau4005 |
[19]
.” Notice the wide tolerance, with total neutron mass falling anywhere between 2.6
M⊙ and 6.1
M⊙!
3.3. Conventional Approach to the Density Question
Historical motivation for determining total mass. A long-sought goal, in theoretical physics, has been to establish the
equation of state of aggregate neutron matter. This important equation essentially quantifies the density of these stars. One of its key components is the total mass. And so, the strategy has been to determine empirically the mass limit of neutron stars and also, somehow, obtain their physical size. It then becomes possible to establish the equation of state of bulk neutron matter
| [20] | Gursky, H., as in Frontiers of Astrophysics, Eugene H. Avrett, editor, (Harvard University Press, Cambridge, Massachusetts, 1977). P197. |
[20]
. Hence, there is an ongoing search for high-mass compact objects.
The density within neutron stars is, of course, extraordinarily high. For non-critical-state neutron stars the matter ranges from atomic nuclei embedded in a sea of electrons at moderate densities in the outer layer, to increasingly neutron-rich composition in the middle layers, to the extremely neutron-rich matter in the core. And, as some theorists have speculated, there might be an even higher density associated with some exotic quark-state of matter at the inner core. Quarks, however, are more symbolic than they are real. Under the enlightened view, they do not exist —not as actual particles. According to the reality-based theory of particles advanced by physicist Graeme Williamson
quarks are simply not necessary. Regardless of the composition of the matter, the concern here is with the ultimate state of its compression.
As stated earlier, two forces, the neutron degeneracy pressure and the repulsive strong force, counter the crushing gravitational effect, which itself varies with the total mass content. Clearly, then, the mass density must vary. Accordingly, the greater the total mass, the greater is the density. And the traditional approach has been a matter of finding the most massive neutron star and determine its equation of state (that is, find a relationship between its mass, radius, and volume). But if the goal is to find the absolute maximum density, that strategy would fail.
It turns out that the ultimate density is not to be found among high-mass compact bodies.
4. Determining Nature’s Ultimate Density
4.1. Empirical Fact
Instead of looking for the most massive neutron star and estimating its diameter and struggling with its equation of state, the method here will be to make use of a remarkable empirical fact: The vast majority of neutron stars are identical. The overwhelming number of neutron stars possess the same quantity of mass — namely 1.4 M⊙. Astronomers have repeatedly noted, “When the masses of neutron stars are measured precisely, they are all around 1.4 solar masses.”... Also noted has been the fact that very few high-mass ones are found; neutron stars above 2.2 solar masses are rare. Clearly, this pattern is not indicative of some statistical aspect. Something special is involved here, something of key importance.
The reason for this one-size dominance in the population is plainly evident in
Figure 2. In the evolutionary life of neutron stars, all end up as End-State stars. Regardless of how a neutron star initially formed, regardless of what mechanism brought it into being, regardless of its evolutionary development, it will always end up as a Terminal star (an End-State neutron star). There is no exception. (The only variance within the neutron class of stars is among its pre-collapsed members — pre-end-state-collapsed members.)
What about the specific size? How is the 1.4 solar mass to be explained? Empirically, it is just the measured value (determined from the gravity dynamics of binary systems). Theoretically, it is determined by Nature’s ultimate mass-density state. And that density is what it is; its value is a built-in constant, just like the speed-of-light-in-vacuum constant.
Now to determine the actual value of that density. We have the mass content; we need the radius. The radius, however, is impossible to measure with any conceivable instruments. It is far, far too small (with a diameter in the neighborhood of 10 km); it is often hidden deep within an accretion disc; and the distance from the Earth is staggering. Moreover, even in the absence of an obscuring disc, Terminal stars are practically invisible; except for polar emissions, they radiate no light.
Nevertheless, the radius is essential. Remarkably, there is a straightforward way to find it. This is where the new insight comes into play —the insight associated with DSSU theory, the most successful cosmology theory in terms of multiple criteria.
4.2. Method and Calculations
We make use of the defining feature of an End-State neutron star. Its surface exists in a critical state, which means that the universal space medium (the vacuum) is flowing into the structure’s surface at lightspeed. As specified earlier, this situation entails the presence of a pure energy surface layer consisting of photons and neutrinos (necessarily so, in order to conform to special relativity’s simple rule limiting the relative speed between the outwardly-directed radiation and the inwardly-directed vacuum flow)
| [22] | Ranzan, C. (2020) Law of Physics 20th-Century Scientists Overlooked (Part 2): Energy Generation via Velocity Differential Blueshift. Physics Essays, Vol. 33, No. 3, pp. 289-298. http://dx.doi.org/10.4006/0836-1398-33.3.289 |
[22]
. The basic expression relating the speed (υ
inflow) of the universal-medium inflow and the mass (
M) and radius (
R) of a gravitating structure is:
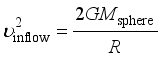
;
| [23] | Ranzan, C. (2018) The Nature of Gravity –How one factor unifies gravity’s convergent, divergent, vortex, and wave effects. International Journal of Astrophysics and Space Science (IJASS), Vol. 6, No. 5, 2018, pp. 73-92. http://dx.doi.org/10.11648/j.ijass.20180605.11 |
[23]
Transformed into the expression for the radius:
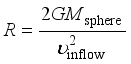
.
(2) The critical radius is easily calculated by substituting values: 3.0×108 m/s (lightspeed) for υinflow; 2.8×1030 kg, which corresponds to 1.4 M⊙, for Msphere; and 6.674×10−11 N∙m2/kg2 for G, the Newtonian gravitational constant. The result is
Criticalradius=4153meters.(3)
The density is simply mass divided by volume (spherical in this case). The critical density is then
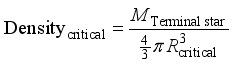
.
(4) The density of a Terminal star works out to be 0.933×1019 kg/m3.
Understand, this represents an absolute maximum density. It has no dependency on rotation! No amount of axial spin can ever cause equatorial bulging and thereby alter the density —physically impossible, as explained in the Discussion section. Moreover, no amount of additional mass can alter the density —again, physically impossible, as explained in Section 6.
An End-State neutron star is truly an unalterable final-fate condition —a fate all neutron bodies are destined to experience.
4.3. Graphical Perspective
The approach here is to make a graph of a range of high-density masses that are defined as being in the critical state. The range of masses so defined, and lying along a drawn curve, is strictly theoretical. A range of such mass objects do not actually exist. However, one mass on this curve does actually exist. One specific point on the theoretical curve represents an ontologically real mass —the End-State neutron object.
Two graphs are examined; one presents mass as a function of the body’s radius; the other presents mass as a function of its density.
Graph of total Mass versus surface Radius:
Startwiththebasicaetherinflowexpression,equation(
1):
Startwiththebasicaetherinflowexpression,equation(
1):
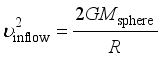
.
Convert to the critical state. The mass parameter, by definition, becomes ‘critical’ Mcrit when the υinflow equals lightspeed c. The inflow expression is then written as
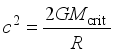
.
(5) Mass criticality as a function of the body’s radius, then, is:
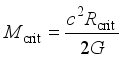
.
(6) As shown in
Figure 3, the critical radius corresponding to the observed 1.4 solar mass is
4.15 kilometers.
Figure 3. Graph of total Mass versus surface Radius. The ‘curve’ represents the mathematically possible critical masses. Indicated is the one point matching the actual Critical-State neutron star —when the radius is 4150 kilometers and the mass is 1.4 M⊙.
Graph of total Mass versus Density:
Since Volume = (4/3)πR3 and volume is by definition M/ρ, the radius of a mass sphere may be expressed as
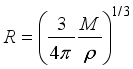
,
(7) where ρ may be uniform or average density.
Substitute equation (
7) into equation (
6) and solve for mass. The resulting expression gives the critical mass in terms of density
ρ:
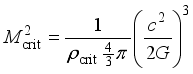
.
(8) The critical-mass function (
8) is graphed in
Figure 4, confirming that the density for the empirically determined End-State 1.4 solar mass is
9.33×1018 kg/m3.
Figure 4. The neutron star possessing Nature’s ultimate density must be found somewhere on the “Theoretical CRITICAL-STATE curve”. To find that point on the curve select the mass associated with the most abundant neutron stars (1.4 M⊙) and draw a horizontal line through the corresponding value on the total mass axis. Where the line meets the curve is where one finds the maximum density (the critical-state mass density).
5. How the Ultimate Density Is Kept Constant
The Mechanism keeping density unalterable.
5.1. Additional Mass
It has been assumed that there exists an ultimate density state; and with a Terminal star this density has been reached. It cannot increase. So, what then happens to any additional mass that will inevitably fall onto/into the structure? The situation is this: Not only is the density unchangeable but so is the overall physical size. It too is unalterable, it cannot grow larger. The reason the End-State neutron star cannot grow larger when more mass is added is a consequence of a simple rule integral to special relativity.
For the explanation, consider a simple example. Say, a one-half solar-mass body is added to a Terminal star. With the density remaining unchanged at 0.933×1019 kg/m3, the new enlarged radius can be calculated as follows.
Since Volsphere = (4/3) πR3 and Volsphere = Mtotal /ρult., where ρult. is the ultimate density, the expression for the radius (Rexperimental) works out to be:
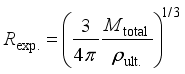
;
(9) With mass 3.8×10
30 kg (corresponding to 1.4
M⊙+0.5
M⊙) and density 0.933×10
19 kg/m3, the
experimental radius works out to be 4598
meters. Now to check, using equation (
1), the speed of the inflowing mass-sustaining aether,
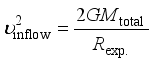
.
(10) This turns out to be 332,000 kilometers per second (or 3.32×108 m/s), which significantly exceeds the speed of light, and is therefore quite impossible. The calculation says that relative motion between the inflowing aether and the surface of the experimental structure exceeds the strict limit imposed by Einstein’s and Lorentz’s relativity.
Unavoidable conclusion: No amount of mass can increase the size of a Terminal star.
Having established that the Terminal star cannot collapse further and cannot grow larger (and become more massive), the question then is, What happens to the additional mass?... Fortunately, there is no need to invoke some unknown new force. No, it’s simply a matter of making use of something already known to exist. The answer lies in the nature of matter itself.
5.2. Mass-Loss by Aether Deprivation Annihilation
The question of the fate of ‘additional mass’ involves not only the nature of matter but also extends into the core of the concept of existence. All matter (all mass and energy particles) absorbs and consumes the universal-space-medium. The very existence of matter depends on an absorption/consumption process. Mass, ontologically speaking, is an energy process that depends on a continuous ‘life-sustaining’ supply of the aether medium. Pictured on the large scale, mass serves as a sink for the medium’s bulk flow. Therein lies the explanation for the inflows (that surround structures) discussed earlier (as well as the explanation for the mechanism of contractile gravity).
It logically follows, if matter/mass is somehow deprived of its essential flow of aether, it must cease to exist
| [24] | Ranzan, C. (2021) Law of Physics 20th-Century Scientists Overlooked (Part 4): Mass Extinction by Aether Deprivation, Journal of High Energy Physics, Gravitation and Cosmology (JHEPGC) Vol. 7, No. 1, pp. 191-209 (2021). https://doi.org/10.4236/jhepgc.2021.71010 |
[24]
. Although locally this represents a violation of energy conservation, on the large scale it does not
| [25] | Ranzan, C. (2021) Law of Physics 20th-Century Scientists Overlooked (Part 6): Law of Cosmic-Scale Conservation of Energy, Physics Essays Vol. 34, No. 3, pp. 331-339 (Sept 2021). http://dx.doi.org/10.4006/0836-1398-34.3.331 |
[25]
.
Aether deprivation is simply an absence of the universal fluid, a chocking-off of aether flow. It is the essential condition whereby matter is extinguished —totally. Since matter cannot exist without aether, it vanishes. The condition occurs only in the interior of critical-state contiguous mass.
Aether deprivation annihilation is the process of total destruction of matter that takes place deep inside extreme mass concentrations. It occurs when mass aggregation reaches a state at which an insufficient quantity of aether reaches the core; and since matter cannot exist in the absence of aether, the aether deficiency results in the terminal annihilation of the affected matter. (When a neutron star gains too much additional mass, it will transform to the critical state, after which its core will become a region of terminal annihilation.)
The
matter extinction law, whereby mass (and energy particles) subjected to aether deprivation ceases to exist, is schematically presented in
Figure 5. One sequence represents piecemeal acquisition or continuous ingesting. Matter falls in, while matter at the center vanishes. But note, they are not one and the same; the in-fallen matter is separated from the vanishing core material by a distance of roughly 2
kilometers. Also be aware that a significant amount of mass is converted to energy which escapes through the Terminal star’s polar emission portals; although, this is not shown in the figure. The other sequence shows the gravitational merger of a pair of Terminal stars. Note that the energy surface/layer never ‘opens-up’; it remains intact throughout the brief duration of the merger. Simultaneously, mass/matter vanishes from the core region.
Figure 5. Matter extinction, a mass loss process resulting from aether deprivation, occurs during gravitational mergers and mass encounters. The schematic sequences show the main features of the mechanism by which Terminal stars maintain their total-mass invariance —their constant quantity of matter— regardless of any accretion rate. As ‘new’ matter falls in, ‘old’ matter vanishes at the core (shown in cross section). What is not shown are the polar emission beams through which great surges and bursts of energy (derived mainly from infalling-mass-to-energy conversion) are emitted during mass accrual.
Recapping. A large portion of whatever quantity of mass that falls onto or into a Terminal star causes, almost instantly, an equivalent amount to vanish at the core. This is literally a disappearance of matter —a process of vanishment from the Universe. Simultaneously, the balance of the ‘input’ material, after undergoing mass-to-energy conversion
| [26] | Ranzan, C. (2020) Law of Physics 20th-Century Scientists Overlooked (Part 3): Noninteraction Mass-to-Energy Conversion, International Journal of High Energy Physics Vol. 7, No. 1, 2020, pp. 19-31 (2020). http://dx.doi.org/10.11648/j.ijhep.20200701.14 |
[26]
, is ejected as radiation energy at the magnetic poles.
6. Discussion
The question of a density gradient. It is quite probable that Terminal stars do not have a density gradient. The expectation is that mass density is maximal from the core all the way to the underside of the energy layer of the surface. But there is really no way of knowing. In any case, this 1-2-3 rule holds: Adding mass to a Terminal star cannot cause a size-collapse; cannot cause a size-enlargement; and cannot cause a density change.
Universal-space-medium. This is the sub-physical fluid permeating all of three-dimensional space. Call it what you wish, the quantum foam (as particle physicists do), the vacuum (as most people do), the space fluid (as a generic term), the dynamic aether (as in DSSU theory), the cosmic fabric and cosmic ocean (as Brian Greene did in his book The Fabric of the Cosmos), the ether Grid (as did Nobelist Frank Wilczek), the Quintessence fluid (as did Tom Siegfried in his book Strange Matters), the Fifth essence (as countless others have done)... Just keep this in mind: It is not a material fluid; in itself, it has no mass and no energy. More specifically, its discrete units/entities possess no mass and no energy (in the conventional sense of their meaning).
Why is this so important? It means that the process, whereby the dynamic aether flows into a neutron star and vanishes (quite literally) therein, does not violate the law of energy conservation. This applies to all mass bodies; it applies to any and all matter. The universal medium that streams into matter, and is consumed by matter in order to sustain its existence, does not contravene the conservation of energy principle.
Nature of the lightspeed boundary. The addition of more and more mass to a stable low-mass neutron star would, according to general relativity theory (as well as DSSU theory), eventually lead to the formation of a lightspeed boundary. This means the surface of the neutron star transforms into pure energy. A thin layer of neutrons undergoes conversion to photonic radiation —which remains trapped within the lightspeed boundary.
Figure 6 shows how this works. While the universal space medium is flowing inward (at lightspeed), the photonic radiation is propagating outward (at lightspeed).
For the details on how such a surface energy layer comes about, how mass actually transitions into pure energy during gravitational collapse, see the journal published articles,
Noninteraction Mass-to-Energy Conversion | [26] | Ranzan, C. (2020) Law of Physics 20th-Century Scientists Overlooked (Part 3): Noninteraction Mass-to-Energy Conversion, International Journal of High Energy Physics Vol. 7, No. 1, 2020, pp. 19-31 (2020). http://dx.doi.org/10.11648/j.ijhep.20200701.14 |
[26]
and
The Nature of Gravitational Collapse .
Without recognizing the true nature of the Terminal star’s surface, one might protest that having the vacuum flowing onto the structure’s surface at the speed of light represents a violation of special relativity. Indeed, from the perspective of the surface, the inflowing aether represents a ‘headwind’ streaming in at lightspeed c; and, conversely, from the perspective of the aether, the surface is speeding into the aether at the same extreme speed. But on close inspection there is no violation. The seeming violation vanishes when it is realized that an End-State neutron star does not have a mass surface. Rather, it has a pure energy layer —consisting of photons and neutrinos which can, and do, propagate at the speed of light. Propagating radially in-place, they are trapped within the surface layer.
Figure 6. Lightspeed boundary envelopes the Terminal star. The radiation particles within the boundary are propagating outward at the speed of light, while the universal space medium is streaming inward with the very same speed. Consequently, the energy particles remain ‘stationary’ with respect to the overall neutron structure; and, thus, the system remains in compliance with the rules of relativity.
Outliers explained. Neutron stars outside the 1.4 M⊙ ‘weight’ category have straightforward explanations. The low mass ones simply do not have enough degenerate mass to achieve the critical state to become a Terminal star. The high mass ones possess significant rotation, which induces a centrifugal effect manifesting as an equatorial bulge (an oblate sphericity). The oblate shape gives the neutron star a greater surface area than it would otherwise have. The greater surface area permits a larger volume of aether inflow. And the larger volume of aether, in turn, allows more mass to exist in the star’s interior. In a nutshell, the faster a neutron star spins, the more mass it can support, the more massive it can be.
In order to become a high-mass-but-subcritical neutron star, it is essential that high rotation rate be acquired BEFORE gaining the excessive mass, the mass over and above the normal 1.4, or 2.2 M⊙, limit. When a fast rotating subcritical neutron star has accreted sufficient mass (or somehow decreased its rotation rate and angular momentum), its surface will become critical and it will collapses to the 1.4 M⊙ end state. It becomes a Terminal star.
Unavoidable consequence. The unavoidable consequence of the existence of a finite ultimate density is this: Stellar black holes do not exist.
It turns out Einstein was right after all. Nature does indeed have some way of preventing ever increasing density, or as he put it, a way of preventing mass to collapse through its Schwarzschild boundary (more descriptively known as the lightspeed event horizon). Einstein well understood there can be no surface of any kind (material or radiant energy) anywhere in the interior deep below a Schwarzschild boundary —there simply cannot be a mass surface inside a Schwarzschild sphere. Why? Because the speed of the vacuum inside far exceeds lightspeed.
Nevertheless, with mathematics a solution can always be found. Thus was born the mass singularity. The gravitating mass becomes a singularity, a mathematical point with zero dimensions and, most importantly, no surface! With mathematical magic, the pros made the surface disappear. And thus, special relativity is satisfied. But there’s a price; their singularity is admittedly a complete unknown.
In 1939, Einstein had published a paper that provided, in his words, “a clear understanding as to why these Schwarzschild singularities do not exist in physical reality
| [28] | Einstein, A. (1939) On a Stationary System with Spherical Symmetry Consisting of Many Gravitating Masses, Annals of Mathematics, 1939. |
[28]
.”
The views of British astronomer Sir Arthur Stanley Eddington and Soviet physicist Lev Landau, as well, proved to be right. They cautioned, some as yet unknown law of nature surely exists to prevent unrestrained collapse.
“Like Eddington, Landau thought this [collapse to infinite density] conclusion was ridiculous and argued that there must be some law of nature, as yet unknown, that would prevent the ultimate collapse.” –John Gribbin and Martin Rees,
Cosmic Coincidences | [29] | Gribbin, J. & Rees, M. (1989) Cosmic Coincidences, Dark Matter, Mankind, and Anthropic Cosmology (Bantam Books, New York, 1989). P157. |
[29]
.
So, if singularities are not real, then neither are stellar black holes.
Supermassive black regions. Although the existence of stellar-size black holes is precluded, it is still possible to have a supermassive non-contiguous mass structure enclosed by a lightspeed boundary (a conventional event horizon). Such a structure consists almost entirely of compact bodies (mostly Terminal stars), and absolutely must be rotating. Think of it as a very crowded collection of dwarf bodies and neutron stars, a miniature rotating system. If there are enough members within a relatively small volume, then a surrounding lightspeed boundary will form.
A supermassive region is a compact rotating galaxy of collapsed stars. If the region becomes sufficiently massive it becomes surrounded by a ‘black’ boundary —a lightspeed horizon where the vacuum flows inward at the full speed of light.
7. Summary & Conclusion
7.1. Overview
By adopting a reasonable assumption on density, the several paradoxes of conventional black hole physics were avoided.
And by recognizing that there must be something deeply significant about this empirical fact: The vast majority of neutron stars are mass rated at 1.4 M⊙.
The two were then conceptually brought together. Combined were the maximal density assumption and the mass-size uniformity. This synthesis led to the concept of surface criticality —the situation where mass density, mass content, and aether inflow speed, all reach a limit. It, thus, became possible to define the End-State neutron star (Terminal star).
Lastly, with the new insight provided by a fundamental feature of DSSU theory —namely, the veritable existence of mass/matter depends totally on a continuous supply of the universal space medium— there emerged a complete picture of the mechanism by which Nature maintains the size-and-density constancy of Terminal stars. At the heart of the mechanism is the principle, or process, of mass extinction by aether deprivation.
Two long-standing mysteries in astrophysics have been resolved: The question of the maximal density of neutron stars and the reason for their single-size population dominance. The implications for cosmology are profound, as can be gathered from
Table 1, which provides a compact comparison and convenient summary of the main ideas, findings, and conclusions presented in this article.
Table 1. The physics of End-State gravitational collapse. This summary of two views gives a point-by-point comparison between the math-based perspective and the natural-process perspective.
End-State Gravitational Collapse |
| 20th-century Mathematical View | Natural Process View (The DSSU) |
Basic collapse: | Self-collapse through the Schwarzschild radius to become a so-called black hole. | Self-collapse to become a Terminal star. Collapse halts when maximum density is attained. |
Lightspeed boundary? | Yes. An encompassing boundary in space called an event horizon. | Yes. A pure energy surface or layer (absent only at the magnetic poles). |
Total mass: | Wide range of mass content predicted. | 1.4 solar mass (M⊙). |
Radius: | Wide range (distance from center to event horizon). | 4153 meters (the critical radius). |
Density: | Infinite density (indicating mathematical breakdown and hypothesis failure). | 0.93×1019 kg/m3. |
What happens to excess or additional mass? | Added to the mathematical core-object called a singularity. | Causes a corresponding quantity to suffer aether deprivation annihilation. (Also causes polar emission of radiation.) |
Explanation for vast dominance of 1.4 M⊙ neutron stars: | Complete mystery. | Yes. |
Energy escape mechanism: | Black holes are purported to evaporate, via thermal radiation, very, very slowly. | Powerful polar emission beams (photons & neutrinos). |
Problems: | 1) The singularity absurdity: the paradox of infinite density mass in a zero-dimensional space! | No problems, theoretical or practical. |
2) The angular momentum paradox. |
3) The gravity paradox: The gravity-causing singularity sucks in everything EXCEPT the energy of its surrounding gravity field!! |
Relationship to Einstein’s view: | Disagrees with Einstein’s view that mass does not collapse through its Schwarzschild size.* | Conforms to Einstein’s view. |
Method for complying with conservation-of-matter law: | 1) Matter is not permanently lost. Mass never ever dies! | 1) Local violation, yes. Global violation, no. |
2) Mass within black holes is mathematically converted to energy and radiated away. | 2) Mass extinction by aether deprivation process is in perpetual cosmic-scale balance with matter-formation process(es). |
The mass-extinction mechanism —based on the principle that when matter (mass and energy) is subjected to aether deprivation, it ceases to exist— is of game-changing importance for research into total gravitational collapse and black-hole physics. The concept of aether deprivation entirely avoids the well-known paradoxes associated with hypothetical black holes. Crucially important to the study of extreme gravity, this simple yet overlooked process circumvents the breakdown of theoretical physics in the context of the conventional 20th-century view of terminal collapse.
7.2. Conclusion
No ‘collapse-preventing’ force is needed. Is this not an ironic situation? The conventional approach uses relativity theory to argue for unlimited gravitational collapse; and yet the more reasonable natural approach uses relativity theory to argue the opposite.
Physicist and popular author Paul Davies summarizes the 20
th-century view: “We now know, from relativity theory, that no force in the Universe can prevent the star from continuing to collapse, once it has reached the light-trapping stage. So the star simply shrinks away, essentially to nothing, leaving behind empty space —a hole where the star once was. But the hole retains the gravitational imprint of the erstwhile star, in the form of intense space and time warps
| [30] | Davies, P. & Gribbin, J. (1992) The Matter Myth (Simon & Schuster, Touchstone, New York, 1992). P265. |
[30]
.”
But, it turns out that no additional force is needed to “prevent the star from continuing to collapse”! Such is not necessary. One just needs to understand this: Matter, whether in the form of mass or radiation particles, cannot exist in the absence of the vital universal ethereal medium. It follows, if some mechanism acts to limit the essential supply, if some system is configured in a way that prevents the aether flow from reaching some corporeal region, then a self-regulating effect comes about —the total quantity of contiguous gravitating mass becomes strictly self-limiting. This allows the existing pressure-force to maintain stability. The pressure inherent in Nature’s maximal density is quite sufficient to counter the gravitational ‘force’ and prevent any further collapse.
On the issue of resolving paradoxes, Stephen Adler of the Institute for Advanced Study in Princeton, New Jersey, had this to say:
“Usually when there are paradoxes it’s not ingenious interpretations that solve them. ... It’s just a fact that the laws of physics have a limited domain, which we don’t know the boundaries of. When you go beyond the boundaries, you find new physics.” –New Scientist (14 July 2018) p 29.
Indeed, the laws, the physics, involved in gravitational collapse have a limited domain. The limit of that domain is determined by Nature’s ultimate density of bulk mass. And the “new physics” is found in the mechanism —a system of utmost simplicity— that maintains ultimate density invariance.
Abbreviations
DSSU | Dynamic Steady State Universe |
Author Contributions
Conrad Ranzan is the sole author. The author read and approved the final manuscript.
Conflicts of Interest
The author declares no conflicts of interest.
References
| [1] |
"The Mechanism driving astrophysical jets has been discovered"
www.cellularuniverse.org/index.htm#PressRelease2018
|
| [2] |
"Unprecedented Unification of Gravity Theory"
www.cellularuniverse.org/index.htm#PressRelease2018-12
|
| [3] |
"How Nature Extracts Energy from Aether"
http://www.cellularuniverse.org/index.htm#PressRelease2019-3
|
| [4] |
"Simple extension of Einstein’s relativity theory radically changes black-hole physics"
www.cellularuniverse.org/index.htm#PressRelease2019-5
|
| [5] |
"Discovery of the Cosmic Law of Energy Conservation"
www.cellularuniverse.org/index.htm#PressRelease2021-7
|
| [6] |
"The Ultimate Source of Energy has been Uncovered – the Mainspring of the Universe Resolved"
www.cellularuniverse.org/index.htm#PressRelease2022-8
|
| [7] |
"Contrary to twentieth-century science, contrary to the big-bang paradigm, our Universe is not running down"
www.cellularuniverse.org/index.htm#PressRelease2023-7
|
| [8] |
Harrison, E.R. (2003) Masks of the Universe, Changing Ideas on the Nature of the Cosmos (2nd ed. Cambridge University Press, Cambridge, UK, 2003). P187.
|
| [9] |
"Neutron Stars"
https://www.astro.princeton.edu/~burrows/classes/403/neutron.stars.pdf
|
| [10] |
ScienceDaily January 16, 2018, How massive can neutron stars be?
https://www.sciencedaily.com/releases/2018/01/180116093650.htm
|
| [11] |
Rezzolla, L.; Most, E.R.; Weih, L.R. (2018) Using Gravitational-wave Observations and Quasi-universal Relations to Constrain the Maximum Mass of Neutron Stars. The Astrophysical Journal, Vol. 852(2): L25 (2018).
https://doi.org/10.3847/2041-8213/aaa401
|
| [12] |
Ranzan, C. (2021) Law of Physics 20th-Century Scientists Overlooked (Part 5): Centrifugal Effect Negation, Applied Physics Research Vol. 13, No. 2, pp. 13-34 (2021).
https://doi.org/10.5539/apr.v13n2p13
|
| [13] |
Doroshenko, V.; Suleimanov, V.; Pühlhofer, G.; & Santangelo, A. (2022) "A strangely light neutron star within a supernova remnant". Nature Astronomy 6, pp. 1444-1451 (2022).
https://doi.org/10.1038/s41550-022-01800-1
|
| [14] |
Saffer, A., et al. (2025) A Lower Mass Estimate for PSR J0348+0432 Based on CHIME/Pulsar Precision Timing. The Astrophysical Journal Letters, Vol. 983, No. 1, L20 (2025).
https://iopscience.iop.org/article/10.3847/2041-8213/adc25e
|
| [15] |
Fonseca, E., et al. (2021) Refined mass and geometric measurements of the high-mass PSR J0740+6620. Astrophysical Journal Letters, Vol. 915, L12 (2021).
https://doi.org/10.3847/2041-8213/ac03b8
|
| [16] |
Croswell, K. (2022-7-22) "The heaviest neutron star on record is 2.35 times the mass of the sun". Science News. Retrieved 2022-7-25.
|
| [17] |
Romani, R.W.; Kandel, D.; Filippenko, A.V.; Brink, T.G.; Zheng, W. (2022) "PSR J0952−0607: The Fastest and Heaviest Known Galactic Neutron Star". The Astrophysical Journal Letters, Vol. 934, (2): L17 (2022-7-11).
https://doi.org/10.3847/2041-8213/ac8007
|
| [18] |
Barr, E.D.; Dutta, A.; Freire, P.C.; Cadelano, M.; Gautam, T.; Kramer, M.;... & Possenti, A. (2024) "A pulsar in a binary with a compact object in the mass gap between neutron stars and black holes". Science, 383(6680), (2024) pp. 275-279.
https://www.science.org/doi/abs/10.1126/science.adg3005
|
| [19] |
Thompson, T.A.; Kochanek, C.S.; Stanek, K.Z.; Badenes, C.; [...], and Covey, K. (2019) "A noninteracting low-mass black hole–giant star binary system". Science, Vol. 366, Issue 6465, pp. 637-640 (2019).
https://www.science.org/doi/10.1126/science.aau4005
|
| [20] |
Gursky, H., as in Frontiers of Astrophysics, Eugene H. Avrett, editor, (Harvard University Press, Cambridge, Massachusetts, 1977). P197.
|
| [21] |
Williamson, J.G. (2008) On the nature of the electron and other particles, Presentation at The Cybernetics Society 40th Anniversary Annual Conference (2008 Sept 20) in London.
https://www.researchgate.net/publication/267370968
|
| [22] |
Ranzan, C. (2020) Law of Physics 20th-Century Scientists Overlooked (Part 2): Energy Generation via Velocity Differential Blueshift. Physics Essays, Vol. 33, No. 3, pp. 289-298.
http://dx.doi.org/10.4006/0836-1398-33.3.289
|
| [23] |
Ranzan, C. (2018) The Nature of Gravity –How one factor unifies gravity’s convergent, divergent, vortex, and wave effects. International Journal of Astrophysics and Space Science (IJASS), Vol. 6, No. 5, 2018, pp. 73-92.
http://dx.doi.org/10.11648/j.ijass.20180605.11
|
| [24] |
Ranzan, C. (2021) Law of Physics 20th-Century Scientists Overlooked (Part 4): Mass Extinction by Aether Deprivation, Journal of High Energy Physics, Gravitation and Cosmology (JHEPGC) Vol. 7, No. 1, pp. 191-209 (2021).
https://doi.org/10.4236/jhepgc.2021.71010
|
| [25] |
Ranzan, C. (2021) Law of Physics 20th-Century Scientists Overlooked (Part 6): Law of Cosmic-Scale Conservation of Energy, Physics Essays Vol. 34, No. 3, pp. 331-339 (Sept 2021).
http://dx.doi.org/10.4006/0836-1398-34.3.331
|
| [26] |
Ranzan, C. (2020) Law of Physics 20th-Century Scientists Overlooked (Part 3): Noninteraction Mass-to-Energy Conversion, International Journal of High Energy Physics Vol. 7, No. 1, 2020, pp. 19-31 (2020).
http://dx.doi.org/10.11648/j.ijhep.20200701.14
|
| [27] |
Ranzan, C. (2016) The Nature of Gravitational Collapse, American Journal of Astronomy and Astrophysics. Vol. 4, No. 2, 2016, pp. 15-33.
http://dx.doi.org/10.11648/j.ajaa.20160402.11
|
| [28] |
Einstein, A. (1939) On a Stationary System with Spherical Symmetry Consisting of Many Gravitating Masses, Annals of Mathematics, 1939.
|
| [29] |
Gribbin, J. & Rees, M. (1989) Cosmic Coincidences, Dark Matter, Mankind, and Anthropic Cosmology (Bantam Books, New York, 1989). P157.
|
| [30] |
Davies, P. & Gribbin, J. (1992) The Matter Myth (Simon & Schuster, Touchstone, New York, 1992). P265.
|
Cite This Article
-
APA Style
Ranzan, C. (2025). Nature’s Maximal Mass Density and the Mechanism Keeping It Constant. International Journal of Astrophysics and Space Science, 13(3), 94-105. https://doi.org/10.11648/j.ijass.20251303.13
 Copy
|
Copy
|
 Download
Download
ACS Style
Ranzan, C. Nature’s Maximal Mass Density and the Mechanism Keeping It Constant. Int. J. Astrophys. Space Sci. 2025, 13(3), 94-105. doi: 10.11648/j.ijass.20251303.13
 Copy
|
Copy
|
 Download
Download
AMA Style
Ranzan C. Nature’s Maximal Mass Density and the Mechanism Keeping It Constant. Int J Astrophys Space Sci. 2025;13(3):94-105. doi: 10.11648/j.ijass.20251303.13
 Copy
|
Copy
|
 Download
Download
-
@article{10.11648/j.ijass.20251303.13,
author = {Conrad Ranzan},
title = {Nature’s Maximal Mass Density and the Mechanism Keeping It Constant
},
journal = {International Journal of Astrophysics and Space Science},
volume = {13},
number = {3},
pages = {94-105},
doi = {10.11648/j.ijass.20251303.13},
url = {https://doi.org/10.11648/j.ijass.20251303.13},
eprint = {https://article.sciencepublishinggroup.com/pdf/10.11648.j.ijass.20251303.13},
abstract = {A belief shared by Albert Einstein and by Sir Arthur Stanley Eddington involved the probable existence of some unrecognized law of nature that prevents unrestricted gravitational collapse. The present article builds on this belief by making the reasonable assumption that Nature imposes an absolute limit on the density of mass. This premise of an ultimate density state becomes the key to resolving the mystery of why the overwhelming number of neutron stars have the same total mass value. The mystery involves the long-standing question, Why is there this amazing over-representation of neutron bodies measuring 1.4 solar mass? It turns out these identically-massed bodies are the neutron stars that have acquired a critical-state surface and, so, have reached their final (and identical) evolutionary state —and are recognized as End-State neutron stars. Then, using conventional physics, the radius, volume, and density immediately follow. Finally, by incorporating the simple mass-annihilation mechanism from DSSU theory (currently the most advanced problem-free cosmology), it is revealed how the Terminal state is maintained —how, regardless of the mass quantity an End-State neutron star absorbs, its total mass of 1.4 solar mass never ever changes!},
year = {2025}
}
 Copy
|
Copy
|
 Download
Download
-
TY - JOUR
T1 - Nature’s Maximal Mass Density and the Mechanism Keeping It Constant
AU - Conrad Ranzan
Y1 - 2025/08/05
PY - 2025
N1 - https://doi.org/10.11648/j.ijass.20251303.13
DO - 10.11648/j.ijass.20251303.13
T2 - International Journal of Astrophysics and Space Science
JF - International Journal of Astrophysics and Space Science
JO - International Journal of Astrophysics and Space Science
SP - 94
EP - 105
PB - Science Publishing Group
SN - 2376-7022
UR - https://doi.org/10.11648/j.ijass.20251303.13
AB - A belief shared by Albert Einstein and by Sir Arthur Stanley Eddington involved the probable existence of some unrecognized law of nature that prevents unrestricted gravitational collapse. The present article builds on this belief by making the reasonable assumption that Nature imposes an absolute limit on the density of mass. This premise of an ultimate density state becomes the key to resolving the mystery of why the overwhelming number of neutron stars have the same total mass value. The mystery involves the long-standing question, Why is there this amazing over-representation of neutron bodies measuring 1.4 solar mass? It turns out these identically-massed bodies are the neutron stars that have acquired a critical-state surface and, so, have reached their final (and identical) evolutionary state —and are recognized as End-State neutron stars. Then, using conventional physics, the radius, volume, and density immediately follow. Finally, by incorporating the simple mass-annihilation mechanism from DSSU theory (currently the most advanced problem-free cosmology), it is revealed how the Terminal state is maintained —how, regardless of the mass quantity an End-State neutron star absorbs, its total mass of 1.4 solar mass never ever changes!
VL - 13
IS - 3
ER -
 Copy
|
Copy
|
 Download
Download
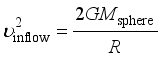 ;
;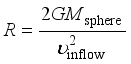 .(2)
.(2) 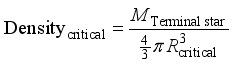 .(4)
.(4) 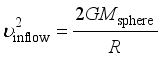 .
. 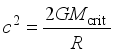 .(5)
.(5) 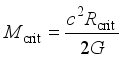 .(6)
.(6) 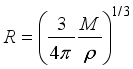 ,(7)
,(7) 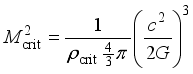 .(8)
.(8) 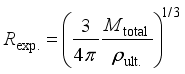 ;(9)
;(9) 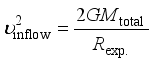 .(10)
.(10)