Lassa virus is transmitted from rodents to humans, but it is not known whether humans can transmit Lassa fever to rats. The virus is thought to spread to humans through contact with contaminated food or surfaces. Other forms of infection include handling rodents for food (people often get rodent blood and urine on their hands) and bites. It can also spread through the use of contaminated medical equipment, such as reusing needles. The state variables of the Lassa Fever model equation is expressed as nonlinear ordinary differential equations in the technique of an initial value problem (IVP) having 10 parameters. As a result of measuring the spread of Lassa fever and determining the stability equilibrium, Lassa fever was found to be stable at an equilibrium point ε0 for which the basic reproduction number R0< 1. This paper optimized three control measures as a means to limit the spread of Lassa fever. The first two measures - regular hand washing and keeping homes and environment clean reduced the rate and impact of transmission between rodents and humans and the treatment of Lassa fever patients reduce transmission to human hosts, which were achieved by the operation of Pontryagin’s Maximum Principle. Therefore, the results of this study demonstrate that the joint control measures adopted in this paper are effective strategies to combat the spread of disease.
| Published in | American Journal of Applied Mathematics (Volume 12, Issue 2) |
| DOI | 10.11648/j.ajam.20241202.11 |
| Page(s) | 24-36 |
| Creative Commons |
This is an Open Access article, distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution and reproduction in any medium or format, provided the original work is properly cited. |
| Copyright |
Copyright © The Author(s), 2024. Published by Science Publishing Group |
Lassa Fever, Scaling, Basic Reproduction Number, Stability Analysis, Controls
2.1. Lassa Fever Model Equations
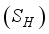 , Exposed
, Exposed 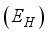 , Infected
, Infected 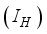 , and Recovered
, and Recovered 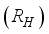 compartments and the rodent populations are divided into two; Susceptible
compartments and the rodent populations are divided into two; Susceptible 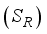 , and Infected
, and Infected 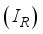 at
at 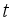 respectively. The susceptible people
respectively. The susceptible people 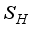 go to the exposed section
go to the exposed section 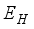 to update population of exposed class to
to update population of exposed class to 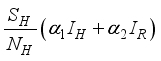 . From the exposed population,
. From the exposed population, 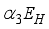 persons are transfer from
persons are transfer from 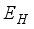 compartment to the infection ward
compartment to the infection ward 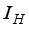 and, as a result of compliance with treatment and prevention measures,
and, as a result of compliance with treatment and prevention measures, 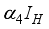 persons move to the recovery group. Finally, the susceptible rodents
persons move to the recovery group. Finally, the susceptible rodents 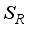 move to the infected compartment
move to the infected compartment 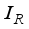 and update the number of infected rodents to
and update the number of infected rodents to 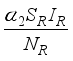 at
at  .
. 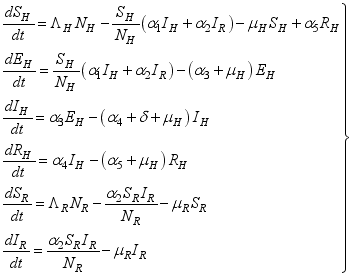 (1)
(1)  (2)
(2) 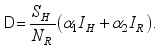
Parameters | Meaning (Dimension: Time-1) |
|---|---|
Recruitment rate for humans | |
Recruitment rate for rodent | |
Contact rate of humans | |
Contact rate of rodents | |
Progression rate to the infectious class | |
Immunity lost rate | |
Rate at which recovered individuals go back to the susceptible class | |
Lassa Fever induced death rate | |
Natural death rate of human | |
Natural death rate of rodents |
2.2. Scaling of the Model
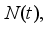 and the ratio of every section within the species is given as:
and the ratio of every section within the species is given as: 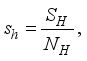
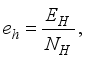
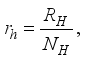
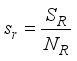
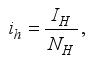
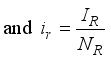 it follows that
it follows that 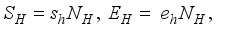
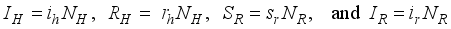 .
. 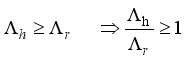 . Let
. Let 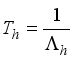 and
and 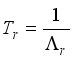
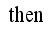
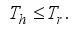 Set
Set 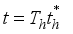 then
then 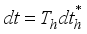 .
. 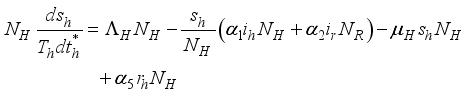
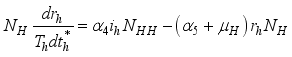
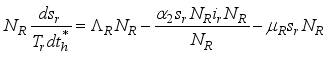
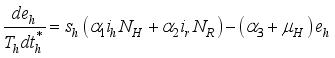
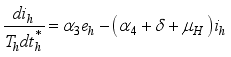
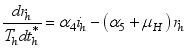
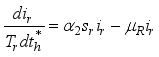
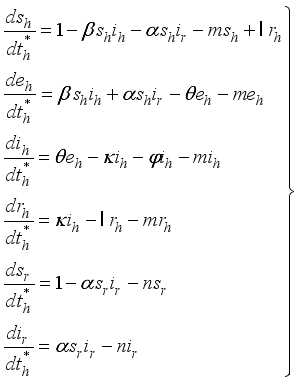 (3)
(3) 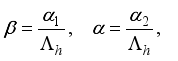
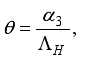
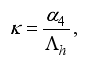
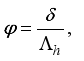
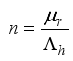
2.3. Lassa Fever Model Properties
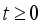 .
. 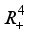 and
and 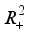 are positively invariant in
are positively invariant in 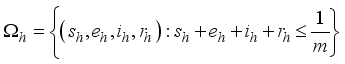 and
and 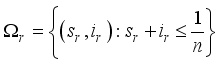
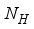 and the class of rodents
and the class of rodents 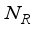 , defined by
, defined by 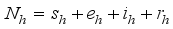 (4)
(4) 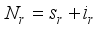 (5)
(5) 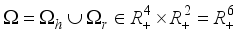
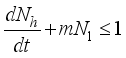
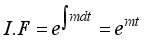
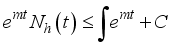
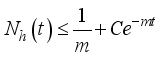
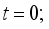 then
then 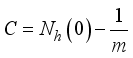
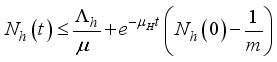
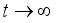
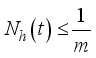 (6)
(6) 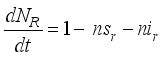
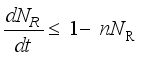
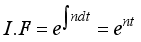
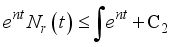
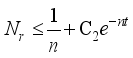
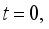
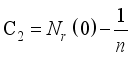
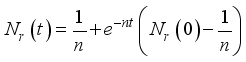
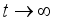
 (7)
(7)  and
and 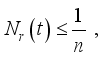 then
then  and
and 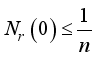 respectively. This is an indication that the solutions of the Lassa Fever model (3) fall in the zone.
respectively. This is an indication that the solutions of the Lassa Fever model (3) fall in the zone. 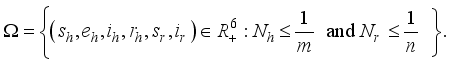
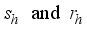 represent the disease-free states and
represent the disease-free states and 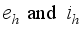 denote the infection class. The Lassa Fever-free equilibrium (LF-FE) point
denote the infection class. The Lassa Fever-free equilibrium (LF-FE) point 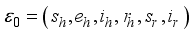 by first setting
by first setting 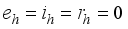 and
and 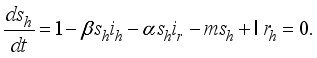
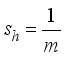 and for the rodents population, the compartments
and for the rodents population, the compartments 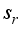 is only the disease-free states and the compartments
is only the disease-free states and the compartments 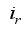 is the infection class,
is the infection class, 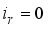 then set
then set 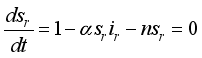 ,
, 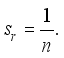 Therefore, the Lassa Fever-free equilibrium (DFE) is
Therefore, the Lassa Fever-free equilibrium (DFE) is 
 of the model equation (3) at
of the model equation (3) at 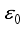 , the application of the next-generation matrix is employed
, the application of the next-generation matrix is employed 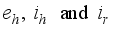 then
then 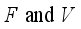 formed the ongoing infection terms and the out sending terms shown below.
formed the ongoing infection terms and the out sending terms shown below. 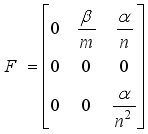
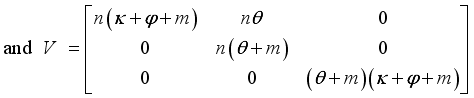
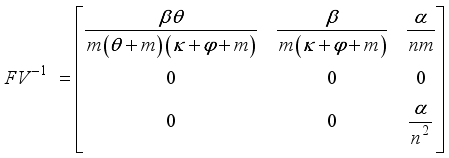
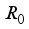 , is obtained from the matrix
, is obtained from the matrix  by calculating it’s spectral radius.
by calculating it’s spectral radius. 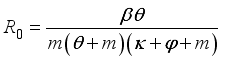
 Theorem 2. When
Theorem 2. When 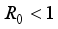 , the Lassa Fever-free equilibrium
, the Lassa Fever-free equilibrium  of the dynamical Lassa Fever equation 3 is locally asymptotically stable.
of the dynamical Lassa Fever equation 3 is locally asymptotically stable. 
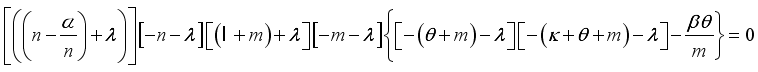
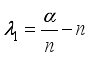
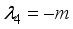
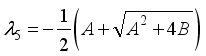
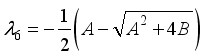
 and
and 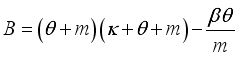
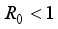 , then
, then  implies
implies  . All eigenvalues will zeros or negatives, hence
. All eigenvalues will zeros or negatives, hence 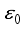 is locally stable. If
is locally stable. If 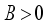 implies
implies  and
and 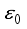 is locally unstable.
is locally unstable. 3.1. Global Stability of Lassa Fever - Free Equilibrium
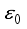 is obtained by applying the approach stated in
is obtained by applying the approach stated in 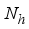 of the Lassa Fever model is defined by
of the Lassa Fever model is defined by 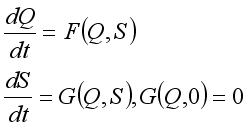
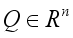 denotes the class of individuals free from Lassa Fever and
denotes the class of individuals free from Lassa Fever and 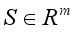 denotes the infected individuals. From the above notation, the Lassa Fever-free equilibrium is written as
denotes the infected individuals. From the above notation, the Lassa Fever-free equilibrium is written as 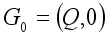 . Then, these two conditions below clearly showed that the global stability of the Lassa Fever free equilibrium.
. Then, these two conditions below clearly showed that the global stability of the Lassa Fever free equilibrium. 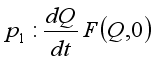 ,
, 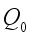 is globally asymptotically stable
is globally asymptotically stable 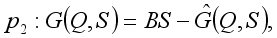 where
where 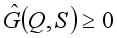 for
for 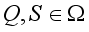
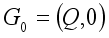 is globally asymptotically stable when
is globally asymptotically stable when 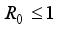 and the above assumptions on
and the above assumptions on 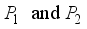 are true.
are true. 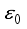 of the Lassa Fever is globally asymptotically stable provided
of the Lassa Fever is globally asymptotically stable provided 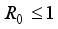 .
. 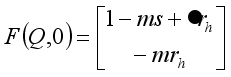
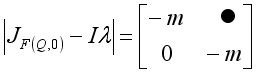
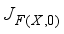 ; we have
; we have 
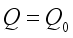 is globally asymptotically stable.
is globally asymptotically stable. 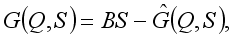
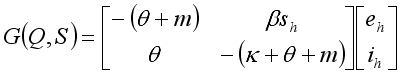
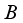 satisfies all conditions stated in
satisfies all conditions stated in 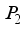 .
. 3.2. Strategy for Prevention of Lassa Fever
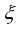 Regular Hand Washing with soap and clean water and food Hygiene; wash vegetables and fruits before eating, properly cover food, Food should be properly cooked, store food in containers with lids or covers, kitchen utensils should be kept clean and covered, avoid hunting and eating of rats will be set to reduce the spread of Lassa fever in the human population.
Regular Hand Washing with soap and clean water and food Hygiene; wash vegetables and fruits before eating, properly cover food, Food should be properly cooked, store food in containers with lids or covers, kitchen utensils should be kept clean and covered, avoid hunting and eating of rats will be set to reduce the spread of Lassa fever in the human population. 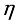 Maintaining a clean Environment at home and the community: keep a cat around, close holes in the house, use of door and window will be set to reduce the breeding of rats in the environment.
Maintaining a clean Environment at home and the community: keep a cat around, close holes in the house, use of door and window will be set to reduce the breeding of rats in the environment. 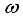 : Treatment of individuals infected with Lassa Fever.
: Treatment of individuals infected with Lassa Fever. 3.3. Lassa Fever Model Equations with Controls
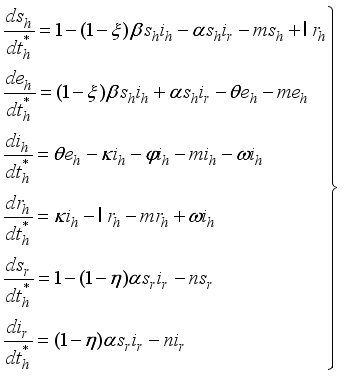 (8)
(8) 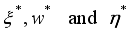 of the controls
of the controls  at time
at time  so that the trajectories which are combined to the states
so that the trajectories which are combined to the states 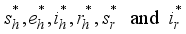 solve the above Lassa Fever model and
solve the above Lassa Fever model and 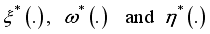 minimizes the function defined below:
minimizes the function defined below: 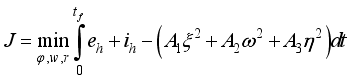 (9)
(9) 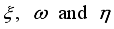 , of the control measures. Here, we employed
, of the control measures. Here, we employed 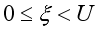 ,
, 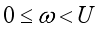 and
and 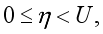 where
where 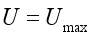 . The conditions required for these optimal controls was obtained by the application of Pontraygin’s Maximum Principle (PMP) is employed
. The conditions required for these optimal controls was obtained by the application of Pontraygin’s Maximum Principle (PMP) is employed 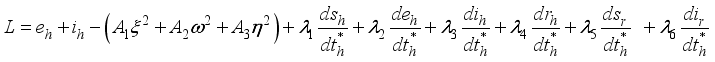
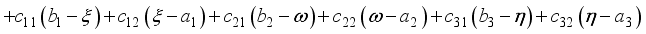
 are penalty multipliers, which satisfy
are penalty multipliers, which satisfy 
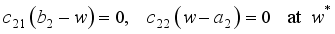
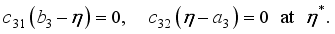
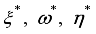 and solution
and solution  of the corresponding state system 8, there exist adjoint variables
of the corresponding state system 8, there exist adjoint variables 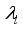 where
where 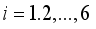
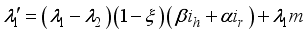
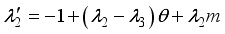
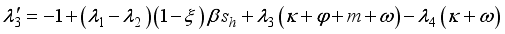
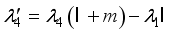
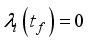 , transversality condition.
, transversality condition. 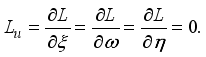
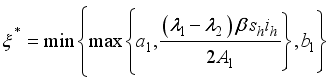
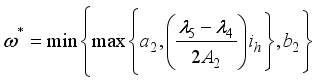
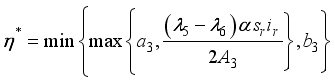
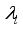 were solved in the system in the Lagrangian.
were solved in the system in the Lagrangian. 

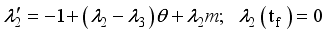
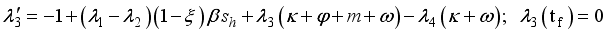
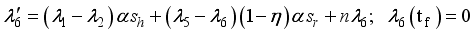
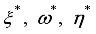 were resolved from
were resolved from 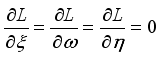 , it follows that,
, it follows that, 
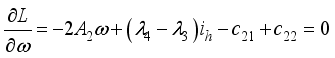
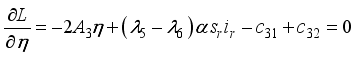
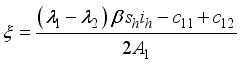
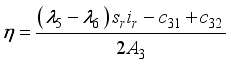
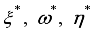 respectively at time
respectively at time  .
. 
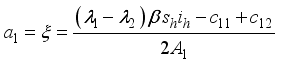
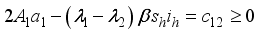
 ,
, 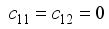
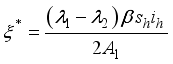
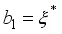 , since
, since 
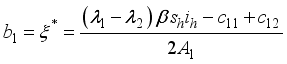
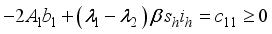
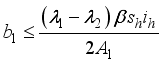
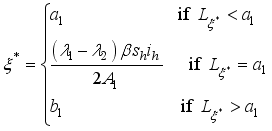
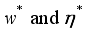 , it follows that
, it follows that 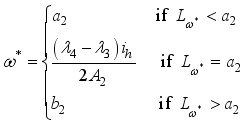
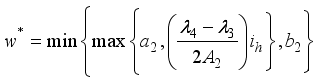
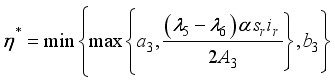
Parameters | Range | Reference | Scale Parameters | Values |
|---|---|---|---|---|
1000*0.0003465 | [17] | 0.069-0.101 | ||
0.05 | [20] | 0.063-0.12 | ||
0.022-0.27 | [17] | 0.001 | ||
0.024-0.048 | [17] | 0.4329 | ||
0.333 | Assumed | 0.961 | ||
0.333-0.8 | [19] | 0.0095 | ||
0.00385 | [19] | 0.00056 | ||
0.00019231 | [18] | 0.12821 | ||
0.0003465 | [18] | |||
0.00641026 | [19] |
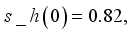
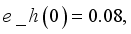
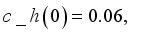
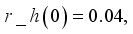
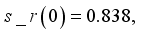 and
and 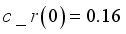 were used. The graph below shows the Model simulation for some period of time. A numerical approach known as the Forward-Backward Sweep method was used to enable numerical modeling of the state and adjoint equations, and MATLAB script was to iteratively update the control by implementing the fourth-order Runge-Kutta method. This state is repeated until successive iterations are sufficiently close to each other
were used. The graph below shows the Model simulation for some period of time. A numerical approach known as the Forward-Backward Sweep method was used to enable numerical modeling of the state and adjoint equations, and MATLAB script was to iteratively update the control by implementing the fourth-order Runge-Kutta method. This state is repeated until successive iterations are sufficiently close to each other 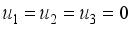
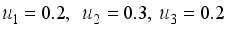
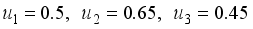
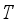 denote the objective function trajectory when
denote the objective function trajectory when 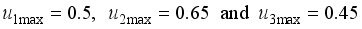 respectively.
respectively. | [1] | Richmond, J. K., Baglole, D. J. Lassa fever: epidemiology, clinical features and social consequences, Bristish Medical Journal, Vol 327, pp 1271-1275, 2003. |
| [2] |
Nigeria Centre for Disease Control. An update of Lassa fever outbreak in Nigeria, June 2021.
https://ncdc.gov.Ng/diseases/sitreps/?cat=5&name=An%20update%20of%20Lassa%20fever%20outbreak%20in%20NigeriaU3 (accessed 17 July 2023). |
| [3] | Ilori, E. A., Furuse, Y., Ipadeola, O. B., Dan-Nwafor, C. C., Abubakar, A., Womi-Eteng, O. E... Ihekweazu, C. Epidemiologic and Clinical Features of Lassa Fever Outbreak in Nigeria, January 1–May 6, 2018. Emerging Infectious Diseases, 25(6), pp. 1066-1074, 2019. |
| [4] | Kehinde Charles Mofolorunsho et al. Outbreak of lassa fever in Nigeria: measures for prevention and control. Pan African Medical Journal. 2016; 23: 210. |
| [5] |
Centre for Disease Control and Prevention. Lassa fever fact sheet. 2022. Available:
http://www.cdc.gov/ncidod/dvrd/spb/mnpages/dispages/factsheets/lassa_fever_fact_sheet.pdf . Accessed August 2023 |
| [6] |
Centre for Disease Control and Prevention. Fact sheet: Lassa fever. 2015. Available:
http://www.cdc.gov/vfh/lassa/pdf/factsheet.pdf . Accessed August 2023. |
| [7] | Patrick N. O., Ifeoma V. N., Onoja A. MATHEMATICAL Model for the Transmission Dynamics of Lassa Fever with Control. Journal/scienceworldjournal.ng. vol. 15, No. 2, 2020. |
| [8] | Hallam, H. J., Hallam, S., Rodriguez, S. E., Barrett A. D. T., David, W. C., Beasley A. C., Chua A., Ksiazek, T. G., Milligan, G. N., Sathiyamoorthy, V., Reece, L. M. ‘Baseline mapping of Lassa fever virology, epidemiology and vaccine research and development’, Nature Partner Journals, Vol 11, pp 1-12, 2018. |
| [9] | Akinpelu F. O., Akinwande R. ‘Mathematical Model for Lassa Fever and Sensitivity Analysis’, Journal of Scientific and Engineering Reseaarch, Vol 5(6), pg 1-9, 2018. |
| [10] | Martins, O.; Moses, M. S.; Dahiru, U.; Abdulkadir, A. Basic Reproductive Number for the Spread and Control of Lassa fever. Int. J. Math. Trends Technol, 30, pp. 1–7, 2016. |
| [11] | Abdulkarim, M. A.; Babale, S. M.; Umeokonkwo, C. D.; Bamgboye, E. A.; Bashorun, A. T.; Usman, A. A.; Balogun, M. S. Epidemiology of Lassa Fever and Factors Associated with Deaths. Emerg. Infect, 26, pp. 799–801, 2020. |
| [12] | Innocent, E. B.; Omo, E. Lassa fever and its Control Measures. Journal of Natural Science Research, vol. 7, 75–79, 2017. |
| [13] | Van den Driessche P. V., Watmough J. “Reproduction number and subthreshold endemic equilibria for compartmental models of disease transmission”. Mathematical Bioscience, vol. 180, pp. 29-48, 2002. |
| [14] | Pontryagin, L. S., Boltyanskii, V. G., Gamkrelidze, R. V., and Mishchenko, E. F. The Mathematical Theory of Optimal Processes, Vol 4, Gordon and Breach Science Publishers, 1986. |
| [15] | Transmission, Signs and Symptoms, Prevention and Treatment of LASSA FEVER for free by MSF (MEDECINS SANS FRONTIERES) medical and humanitarian aid in collaboration with the Ministry Health, Ministry of Environment and the Alex Ekwueme Federal Teaching Hospital Abakaliki (AE-FUNAI). |
| [16] |
Cute Rat population to human population worldwide,
https://a-z-animals.com/blog/how-many-rats-are-in-the-world/ [accessed 27/10/2023]. |
| [17] | Chitnis, N., Hyman, J. M. and Cushing, J. M. “Determining important parameters in the spread of malaria through the sensitivity analysis of a mathematical model,” Bulletin of Mathematical Biology, vol. 70, no. 5, p. 1272, 2008. |
| [18] | World Health Organisation, Lassa Fever-Nigeria, World Health Organization, Geneva, Switzerland, 2016. |
| [19] | Mohammed, B. A., Umar, C. D. and Mamman, M. Sensitivity analysis in a Lassa fever deterministic mathematical model, AIP Conference Proceedings, vol. 1660, 2015. Article ID 050050, |
| [20] | Ogabi, C. O., Olusa, T. V., and Madufor M. A., ‘Controlling Lassa fever transmission in Northern part of Edo state Nigeria using SIS model’, New York Science Journal; 5(12), pp 190 – 197, 2012. |
| [21] | Sunday, N. A. Analyzing Corruption Dynamics and Control Measures in Nigeria: A Mathematical Model. Asian Journal of Pure and Applied Mathematics. Pp. 493-511, 2023. Article no. AJPAM. 1422. |
| [22] | Emmanuel N., Sunday N. A., Louis O., Michael U. “Optimal Control of COVID-19: Examining the Incidence of Contamination and Its Recurrence in Nigeria”. American Journal of Applied Mathematics, vol. 11, pp. 23-31, 2023. |
| [23] | Sunday, N. A., Emmanuel, N., Louis, O. Stability of Covid-19 Dynamics: A Case Study of Nigeria. Britain International of Exact Sciences (BIoEx) Journal. Pp. 173-185, 2023. |
| [24] | Castillo-Chavez C, Song B. Dynamical models of tuberculosis and their applications. Mathematical Bioscience and Engineering, MBE. Vol. 1, No. 2, 2004. |
APA Style
Aloke, S. N., Okpara, P. A. (2024). A Mathematical Model of Lassa Fever Transmission and Control in Ebonyi State, Nigeria. American Journal of Applied Mathematics, 12(2), 24-36. https://doi.org/10.11648/j.ajam.20241202.11
ACS Style
Aloke, S. N.; Okpara, P. A. A Mathematical Model of Lassa Fever Transmission and Control in Ebonyi State, Nigeria. Am. J. Appl. Math. 2024, 12(2), 24-36. doi: 10.11648/j.ajam.20241202.11
AMA Style
Aloke SN, Okpara PA. A Mathematical Model of Lassa Fever Transmission and Control in Ebonyi State, Nigeria. Am J Appl Math. 2024;12(2):24-36. doi: 10.11648/j.ajam.20241202.11
@article{10.11648/j.ajam.20241202.11,
author = {Sunday Nwokpoku Aloke and Patrick Agwu Okpara},
title = {A Mathematical Model of Lassa Fever Transmission and Control in Ebonyi State, Nigeria
},
journal = {American Journal of Applied Mathematics},
volume = {12},
number = {2},
pages = {24-36},
doi = {10.11648/j.ajam.20241202.11},
url = {https://doi.org/10.11648/j.ajam.20241202.11},
eprint = {https://article.sciencepublishinggroup.com/pdf/10.11648.j.ajam.20241202.11},
abstract = {Lassa virus is transmitted from rodents to humans, but it is not known whether humans can transmit Lassa fever to rats. The virus is thought to spread to humans through contact with contaminated food or surfaces. Other forms of infection include handling rodents for food (people often get rodent blood and urine on their hands) and bites. It can also spread through the use of contaminated medical equipment, such as reusing needles. The state variables of the Lassa Fever model equation is expressed as nonlinear ordinary differential equations in the technique of an initial value problem (IVP) having 10 parameters. As a result of measuring the spread of Lassa fever and determining the stability equilibrium, Lassa fever was found to be stable at an equilibrium point ε0 for which the basic reproduction number R0< 1. This paper optimized three control measures as a means to limit the spread of Lassa fever. The first two measures - regular hand washing and keeping homes and environment clean reduced the rate and impact of transmission between rodents and humans and the treatment of Lassa fever patients reduce transmission to human hosts, which were achieved by the operation of Pontryagin’s Maximum Principle. Therefore, the results of this study demonstrate that the joint control measures adopted in this paper are effective strategies to combat the spread of disease.
},
year = {2024}
}
TY - JOUR T1 - A Mathematical Model of Lassa Fever Transmission and Control in Ebonyi State, Nigeria AU - Sunday Nwokpoku Aloke AU - Patrick Agwu Okpara Y1 - 2024/04/02 PY - 2024 N1 - https://doi.org/10.11648/j.ajam.20241202.11 DO - 10.11648/j.ajam.20241202.11 T2 - American Journal of Applied Mathematics JF - American Journal of Applied Mathematics JO - American Journal of Applied Mathematics SP - 24 EP - 36 PB - Science Publishing Group SN - 2330-006X UR - https://doi.org/10.11648/j.ajam.20241202.11 AB - Lassa virus is transmitted from rodents to humans, but it is not known whether humans can transmit Lassa fever to rats. The virus is thought to spread to humans through contact with contaminated food or surfaces. Other forms of infection include handling rodents for food (people often get rodent blood and urine on their hands) and bites. It can also spread through the use of contaminated medical equipment, such as reusing needles. The state variables of the Lassa Fever model equation is expressed as nonlinear ordinary differential equations in the technique of an initial value problem (IVP) having 10 parameters. As a result of measuring the spread of Lassa fever and determining the stability equilibrium, Lassa fever was found to be stable at an equilibrium point ε0 for which the basic reproduction number R0< 1. This paper optimized three control measures as a means to limit the spread of Lassa fever. The first two measures - regular hand washing and keeping homes and environment clean reduced the rate and impact of transmission between rodents and humans and the treatment of Lassa fever patients reduce transmission to human hosts, which were achieved by the operation of Pontryagin’s Maximum Principle. Therefore, the results of this study demonstrate that the joint control measures adopted in this paper are effective strategies to combat the spread of disease. VL - 12 IS - 2 ER -