2. Formulations
In presence of warm positrons, the set of normalized fluid equations for a collisionless, unmagnetized, non-relativistic plasma containing warm positive ions, warm negative ions and two-temperature non-isothermal electrons along with charge neutrality condition are given in the following ways:
++ -=(2)
++ 3= 0(3)
++=(5)
++ 3= 0(6)
Charge neutrality condition is
where
=
=
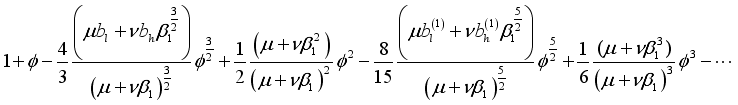 (9)
(9) =,=,=,=,=,
=,=, µ+ν = 1
= , = , = , = ;
For non-isothermal plasma 0 < or < and 0 < or <
In this case, = temperature of free electrons in low temperature, = temperature of free electrons in high temperature, = temperature of trapped electrons in low temperature, = temperature of trapped electrons in high temperature, = effective temperature of electrons, = temperature of positrons, = temperature of positive ions, = temperature of negative ions.
The concerned plasma parameters
,
,
,
,
,
,
,
,
, ϕ, Z,Q, χ,
,x, t, µ, ν,
,
,
,
,
,
and
in equations (
1) to (
10)are respectively the density of positive ions, negative ions, electrons and positrons, the velocity of positive ion and negative ions, the pressure of positive ions and negative ions, the temperature of positive ions and negative ions, the electrostatic potential, charge of ions, mass ratio of negative to positive ions, density of positron at ϕ = 0, temperature ratio of electrons and positrons, distance, time, the unperturbed number density of low temperature and high temperature electrons, the temperature ratio of free electrons in low and high temperatures, the temperature ratio of free and trapped electrons in low temperature, the temperature ratio of free and trapped electrons in high temperatureand the normally used conventional non-isothermal parameters related with
and
.
In this paper the boundary conditions for our systems are
,,,,,,and ф0at
In equations (
1) to (
7), the Galelian transformation η = x – V tis used where V is the velocity of the solitary waves.
Following Chattopadhyay
, the expression for Sagdeev pseudopotential function ψ(ϕ) for two-temperature non-isothermal electron plasmas with warm positive ions, warm negative ions and warm positrons, is obtained as
ψ(ϕ) = [ϕ++......]
+
++(1-) (11)
Where
=(12)
=(13)
The requirements to yield soliton solutions from Sagdeev potential function ψ are
(i) ψ = = 0at φ = 0.
(ii) 0 at φ = 0.
(iii) ψ = 0 at φ = andψ< 0 for 0 < φ <.
(iv) > 0 at φ = 0 for positive (compressive) potential solitons.
(v) > 0 at φ = for positive (compressive) potential solitons.
And the restriction on ϕ is
ф<(14)
Now by using the Galelian transformation and the necessary boundary conditions, it is found from equations (
7), (
9), (
10), (
11), (
12) and (
13) after expansion of ψ(ϕ) in power series
=ϕ++-.......=(15)
And
ψ(ϕ)= -+--(16)
Where
=
=
=
=(17)
In order to get the small amplitude double layer profiles from Sagdeev potential functionψ(ϕ) and small amplitude double layer solutions
, the Sagdeev potential ψ(ϕ)should satisfy the following conditions
:
ψ< 0 for 0 <ϕ<andϕ>(18)
where ( > 0) is some extreme value of the electrostatic potential ϕat which double layer isproduced.
Now taking terms upto
in equation (
15) and
in equation (
16), we get finally after using the above boundary conditions for double layers as
=and=(19)
In terms of
we get finally from equations (
15) and (
16) after simplification as
= -ϕ(21)
=(22)
Where
> 0 represents the stable structure of double layer. Equations (
20) to (
22) give us the first order double layer profile and first order double layer solution.
3. Results and Discussions
In this section, the profiles of Sagdeev potential function ψ(ϕ) against electrostatic potential ϕfor large amplitude solitons and small amplitude double layers are drawn under the variation of different plasma parameters.
In
Figure 1, the profiles of Sagdeev potential function ψ(ϕ) against electrostatic potential ϕfor large amplitude solitary waves are drawn under the variation of the mass ratios (Q) of negative
to positive
ions in presence
of positrons.
Figure 1. Profiles of Sagdeev potential function ψ(ϕ) against ϕ for large amplitude solitary wavesin two temperature non-isothermal electron plasma under the variation of the mass ratios (Q) of negative and positive ions in presence of positronsfor V = 1.601, = 0.4, = 0.2, = , = , = 0.0501, = 0.88, χ = 0.1701, = 0.4101, µ = 0.15, ν = 0.85, = 0.15, = 0.4, = 0.25, = 0.24, = 0.51, Z = 1 whenQ = 1.912, 3.997, 31.746.
In presence of positrons
the curves
for Q = 1.912,
for Q = 3.997 and
for Q = 31.746 are shown in
Figure 1, represent the solitary waves. The maximum value of the electrostatic potential
for large amplitude solitonsis increasing for increasing values of the mass ratios Q. The Sagdeev potential profiles ψ
against ϕ for well shaped solitary waves denoted by
,
and
cut the ϕ axis at
= 0.277666, 0.284871 & 0.287948 respectively in
Figure 1.
Figures 2, 3, 4 and 5 show the profiles of Sagdeev potential function ψ(ϕ) against electrostatic potential ϕfor large amplitude solitary waves under the variation of the phase velocities (V) of solitary waves in presence
of positrons.
Figure 2. Profiles of Sagdeev potential function ψ(ϕ) against ϕ for large amplitude solitary wavesin two temperature non-isothermal electron plasma under the variation of phase velocity (V) in presence of positrons for = 0.4, = 0.2, = , = , = 0.0501, = 0.88 , χ = 0.1701, = 0, 0.4101, µ = 0.15, ν = 0.85, = 0.15, = 0.4, = 0.25, = 0.24, = 0.51, Z = 1, Q =3.997 when V = 1.601.
Figure 3. Profiles of Sagdeev potential function ψ(ϕ) against ϕ for large amplitude solitary waves in two temperature non-isothermal electron plasma under the variation of phase velocity (V) in presence of positrons for = 0.4, = 0.2, = , = , = 0.0501, = 0.88,χ = 0.1701, = 0.4101, µ = 0.15, ν = 0.85, = 0.15, = 0.4, = 0.25, = 0.24, = 0.51, Z = 1, Q =3.997 when V = 1.69445.
The Sagdeev potential function ψ
against ϕ for large amplitude solitary waves denoted by
in presence of positrons
for V = 1.601 with
=
,
=
is shown in
Figure 2 whereas the curve
in presence of positrons
for V = 1.69445 with
=
,
=
isshown in
Figure 3. It is seen from
Figure 3 that the curve
does not show any actual well shaped solitary waves for V = 1.69445 whereas the curve
in
Figure 2 cuts the ϕ axisat
= 0.284871showing the actual well shaped soliton nature.In
Figure 3, the curve
does not cut the ϕ axis which shows no solitonic structure.Under this different values of V,
Figures 2 and 3 present whether the well shaped nature of soliton will form or not.
Figure 4. Profiles of Sagdeev potential function ψ(ϕ) against ϕ for large amplitude solitons in two temperature non-isothermal electrons under the variation of phase velocity (V) in presence of positron for = 0.5, = 0.3, = , = , = 0.0501, = 0.88,χ = 0.1701, = 0.4101, µ = 0.15, ν = 0.85, = 0.15, = 0.4, = 0.25, = 0.24, = 0.51, Z = 1, Q =3.997 when V = 1.601.Profiles of Sagdeev potential function ψ(ϕ) against ϕ for large amplitude solitons in two temperature non-isothermal electrons under the variation of phase velocity (V) in presence of positron for = 0.5, = 0.3, = , = , = 0.0501, = 0.88,χ = 0.1701, = 0.4101, µ = 0.15, ν = 0.85, = 0.15, = 0.4, = 0.25, = 0.24, = 0.51, Z = 1, Q =3.997 when V = 1.601.
Figure 5. Profiles of Sagdeev potential function ψ(ϕ) against ϕ for large amplitude solitary waves in two temperature non-isothermal electron plasma under the variation of phase velocity (V) in presence of positrons for = 0.5, = 0.3, = , = , = 0.0501, = 0.88,χ = 0.1701, = 0.4101, µ = 0.15, ν = 0.85, = 0.15, = 0.4, = 0.25, = 0.24, = 0.51, Z = 1, Q =3.997 when V = 1.69445.Profiles of Sagdeev potential function ψ(ϕ) against ϕ for large amplitude solitary waves in two temperature non-isothermal electron plasma under the variation of phase velocity (V) in presence of positrons for = 0.5, = 0.3, = , = , = 0.0501, = 0.88,χ = 0.1701, = 0.4101, µ = 0.15, ν = 0.85, = 0.15, = 0.4, = 0.25, = 0.24, = 0.51, Z = 1, Q =3.997 when V = 1.69445.
In
Figure 4, the sagdeev potential profile ψ
against electrostatic potential ϕfor large amplitude solitary waves in presence of positrons
is denoted by the curve
when the temperature of positive
and negative
ions are
=
and
=
with V = 1.601,
= 0.5,
= 0.3. The curve
cuts the φ axis at
= 0.17862 showing their soliton nature.
In
Figure 5, the profile of sagdeev potential function ψ
against electrostatic potential ϕfor large amplitude solitons in presence of positrons
is denoted by
when the temperatures of positive
and negative
ions are
=
and
=
with V = 1.69445,
= 0.5,
= 0.3. In presence of positrons
the curve
cuts the ϕ axis at
= 0.342575 showing the actual well shaped soliton nature.
Similarly it is further found that the profiles of sagdeev potential function ψ against electrostatic potential ϕfor large amplitude solitons in presence of positronsdo not form the actual well shape for any value of ϕ within the limit for the solitary wave condition when the temperature of positive and negative ions are = and = with V = 1.701, 1.801, 1.901& 1.99631, = 0.4, = 0.2, χ = 0.1701, = 0.4101.
Figure 6 represents the Sagdeev potential profiles ψ(ϕ) against electrostatic potential ϕ for large amplitude solitary waves under the variation of the concentrations of negative ions
in presence
of positrons.
Figure 6. Profiles of Sagdeev potential function ψ(ϕ) against ϕ for large amplitude solitary wavesin two temperature non-isothermalelectron plasma under the variation ofthe negative ion concentrations in presence of positrons for = 0.4, = 0.2, = , = , χ = 0.1701, = 0.4101, µ = 0.15, ν = 0.85, = 0.15, = 0.4, = 0.25, = 0.24, = 0.51, Z =1, Q = 1.912, V = 1.601, = 0.8299, 0.88 when = 0, 0.0501.Profiles of Sagdeev potential function ψ(ϕ) against ϕ for large amplitude solitary wavesin two temperature non-isothermalelectron plasma under the variation ofthe negative ion concentrations in presence of positrons for = 0.4, = 0.2, = , = , χ = 0.1701, = 0.4101, µ = 0.15, ν = 0.85, = 0.15, = 0.4, = 0.25, = 0.24, = 0.51, Z =1, Q = 1.912, V = 1.601, = 0.8299, 0.88 when = 0, 0.0501.
In presence of positrons, the sagdeev potential profiles ψ(ϕ) against the electrostatic potential ϕfor large amplitude solitary waves are denoted by for = 0 and for = 0.0501when V = 1.601, = 0.4, = 0.2, = , = . The curves and cut the ϕ axis at = 0.297416 and = 0.277660 respectively showing their well shaped soliton nature. This shows the effect of concentrations of negative ions on Sagdeev potential function ψ(ϕ)in presence of positrons.
Figure 7. Profiles of Sagdeev potential function ψ(ϕ) against ϕ for large amplitude solitary wavesin two temperature non-isothermal electron plasma under the variation of the negative ion concentrations in presence of positrons for = 0.4, = 0.2, = , = , χ = 0.1701, = 0.4101,µ = 0.15, ν = 0.85, = 0.15, = 0.4, = 0.25, = 0.24, = 0.51, Z =1, 0; Q = 1.912,V = 1.601, =0.84, 0.9 when = 0.0101, 0.0901.
In
Figure 7, the sagdeev potential function ψ(ϕ) against the electrostatic potential ϕ for large amplitude solitary wavesin presence
of positronsare denoted by
for
= 0.0101 and
for
= 0.0901 whenV = 1.601,
= 0.4,
= 0.2,
=
,
=
. It is evident from this figure that the curve
for
= 0.0101 cuts the ϕ axis at a larger distance than the curve
for
= 0.0901 with χ = 0.1701 where the curve
cuts the ϕ axis at
= 0.259325. The
Figures 6 and 7 show the characteristics of the sagdeev potential function under the variation of the concentration of negative ions
in presence
of positrons.
In
Figure 8, the profiles of Sagdeev potential function ψ(ϕ) against the electrostatic potential ϕ for large amplitude solitary waves are drawn under the variation of the concentrations of positrons(χ). For different values of the concentrations of positrons
, the sagdeev potential function ψ
cuts the ϕ axis at different values. The sagdeev potential function ψ
at χ = 0.0801 denoted by
cuts the ϕ axis at
= 0.213413 and at χ = 0.1201, the sagdeev potential function ψ
denoted by
cuts the ϕ axis at
= 0.246681. The curve
represents the sagdeev potential function ψ
cuts the ϕ axis at
= 0.277660 for χ = 0.1701 which is larger than all other values.
Figure 8. Profiles of Sagdeev potential function ψ(ϕ) against ϕ for large amplitude solitary waves in two temperature non-isothermal electron plasma under the variation of the concentrations of positrons for V = 1.601, = 0.4, = 0.2, = , = , = 0.0501, =1.0501, 0.97, 0.93,0.88, = 0, 0.4101,µ = 0.15, ν = 0.85, = 0.15, = 0.4, = 0.25, = 0.24, = 0.51, Z =1,Q = 1.912 when χ =0.0801, 0.1201,0.1701.
Figure 9. Profiles of Sagdeev potential function ψ(ϕ) against ϕ for large amplitude solitons in two temperature non-isothermal electrons under the variation of the temperature ratios of electrons and positrons for V = 1.601, = 0.4, = 0.2, = , = , = 0.0501, =0.88, χ =0.1701,µ = 0.15, ν = 0.85, = 0.15, = 0.4, = 0.25, = 0.24, = 0.51, Z =1,Q = 1.912 when = 0.4101, 1.Profiles of Sagdeev potential function ψ(ϕ) against ϕ for large amplitude solitons in two temperature non-isothermal electrons under the variation of the temperature ratios of electrons and positrons for V = 1.601, = 0.4, = 0.2, = , = , = 0.0501, =0.88, χ =0.1701,µ = 0.15, ν = 0.85, = 0.15, = 0.4, = 0.25, = 0.24, = 0.51, Z =1,Q = 1.912 when = 0.4101, 1.
In
Figure 9, the Sagdeev potential profiles ψ(ϕ) against the electrostatic potential ϕ for large amplitude solitons are drawn under the variation of the different temperature ratios
of electron
and positron
. It is observed from
Figures 9 and 10 that the Sagdeev potential profiles cut the ϕ axis at larger distances as long as the temperature ratios
ofelectron
and positron
is increasing. The Sagdeev potential profiles ψ(ϕ) against ϕfor solitary waves are denoted respectively by the curves
for
= 0.4101,
for
= 1 in
Figure 9 and
for
= 1.301,
for
= 1.9501 in
Figure 10. In
Figure 9, the Sagdeev potential curves for actual well shaped solitary waves denoted by
for
= 0.4101 cuts the ϕ axis at
= 0.277660,
for
= 1 cuts the ϕ axis at
= 0.307871 but in
Figure 10, for
= 1.301 and 1.9501 no solitary waves for actual well shaped are found and thus it is concluded that for
> 1 no proper solitary waves are found in two-temperature non-isothermal electron plasmas in presence of negative ions.
Figure 10. Profiles of Sagdeev potential function ψ(ϕ) against ϕ for large amplitude solitons in two temperature non-isothermal electrons under the variation of the temperature ratios of electrons and positrons for V = 1.601, = 0.4, = 0.2, = , = , = 0.0501, =0.88,χ =0.1701, µ = 0.15, ν = 0.85, = 0.15, = 0.4, = 0.25, = 0.24, = 0.51, Z =1, Q = 1.912 when = 1.301, 1.9501.Profiles of Sagdeev potential function ψ(ϕ) against ϕ for large amplitude solitons in two temperature non-isothermal electrons under the variation of the temperature ratios of electrons and positrons for V = 1.601, = 0.4, = 0.2, = , = , = 0.0501, =0.88,χ =0.1701, µ = 0.15, ν = 0.85, = 0.15, = 0.4, = 0.25, = 0.24, = 0.51, Z =1, Q = 1.912 when = 1.301, 1.9501.
In the next part, we are now presenting graphically the profiles of small amplitude double layers in presence of positrons under the variation of some plasma parameters.
In
Figure 11, the profiles of Sagdeev potential function ψ(ϕ) against the electrostatic potential ϕ for small amplitude double layers are drawn in presence
of positrons under the variation of the phase velocity (V) of solitary waves. In presence of positrons (χ = 0.1701), the Sagdeev potential profiles ψ(ϕ) against ϕ for small amplitude double layers are denoted by
for V = 1.6501,
for V = 1.6801. It is evident from the figure that for increasing values of V, the maximum values of the electrostatic potential (
) where the respective curves cut the ϕ axis are larger.
Figure 11. Profile of Sagdeev potential functionψ(ϕ) against ϕ for small amplitude double layers in presence of positrons under the variation of phase velocity (V) of solitary waves for = 0.4, = 0.2, = , = , = 0.0501, =0.88, χ =0.1701, = 0.4101,µ = 0.15, ν = 0.85, = 0.15, = 0.4, = 0.25, = 0.24, = 0.51, Z =1,Q = 1.912 when V = 1.6501, V = 1.6801.
Figures 12 and 13 show the profiles of Sagdeev potential function ψ(ϕ) against the electrostatic potential ϕ for small amplitude double layers in presence of positrons
under the variation of the concentrations of negative ions
.In
Figure 12, when the concentration of negative ions is
= 0.0401, the Sagdeev potential profile ψ(ϕ) against ϕ for small amplitude double layers is represented by the curve
for χ = 0.1701 whereas in
Figure 13, when the concentration of negative ions is
= 0.0501, the Sagdeev potential profile ψ(ϕ) against ϕ for small amplitude double layers is denoted by the curve
for χ = 0.1701. In
Figure 12, it is observed that the curve
in presence of positron (χ = 0.1701) cuts the ϕ axis at
= 0.020621 while in
Figure 13, the Sagdeev potential profile ψ(ϕ) against ϕ for small amplitude double layers denoted by the curve
for χ = 0.1701 cuts the ϕ axis at
= 0.342005 when the concentration of negative ions is
= 0.0501.
Figure 13. Profile of Sagdeev potential function ψ(ϕ) against ϕ for small amplitude double layersin presence of positronsunder the variation of the concentration of negative ionsforV = 1.6501, = 0.4, = 0.2, = , = , χ =0.1701, = 0.4101,µ = 0.15, ν = 0.85, = 0.15, = 0.4, = 0.25, = 0.24, = 0.51, Z =1,Q = 1.912, =0.88 when = 0.0501.Profile of Sagdeev potential function ψ(ϕ) against ϕ for small amplitude double layersin presence of positronsunder the variation of the concentration of negative ionsforV = 1.6501, = 0.4, = 0.2, = , = , χ =0.1701, = 0.4101,µ = 0.15, ν = 0.85, = 0.15, = 0.4, = 0.25, = 0.24, = 0.51, Z =1,Q = 1.912, =0.88 when = 0.0501.
Figure 14 shows the profiles of Sagdeev potential function ψ(ϕ) against the electrostatic potential ϕ for small amplitude double layers under the variation of the temperature ratios
of electrons
and positrons
. The Sagdeev potential profiles ψ(ϕ) against ϕ for small amplitude double layers in presence of positron (χ = 0.1701)denoted by
for
= 0.1501 and
for
= 0.4101 cut the ϕ axis at
= 0.322136 and 0.342005 respectively. In this case, it is found that as
increases
also increases.
Figure 14. Profiles of Sagdeev potential function ψ(ϕ) against ϕ for small amplitude double layers in presence of positrons under the variation of the temperature ratios of electrons and positronsfor V = 1.6501, = 0.4, = 0.2, = , = , = 0.0501, =0.88, χ =0.1701, µ = 0.15, ν = 0.85, = 0.15, = 0.4, = 0.25, = 0.24, = 0.51, Z =1,Q = 1.912 when = 0.1501, 0.4101.
From
Figure 14, it is observed that in presence of positron
, the Sagdeev potential profiles ψ
against ϕ for small amplitude double layers cut the ϕ axis at larger values of
for higher values of
while for the smaller values of
the respective Sagdeev potential curves for small amplitude double layerscut the ϕ axis at smaller values of
.
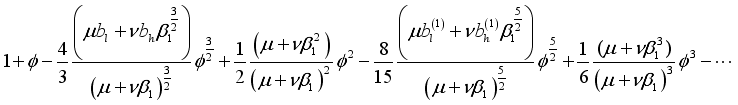 (9)
(9)