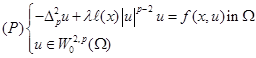-

New Improved Approximation by Linear Combination in Lp Spaces
Issue:
Volume 3, Issue 6, December 2015
Pages:
243-249
Received:
23 August 2015
Accepted:
7 September 2015
Published:
16 October 2015
Abstract: In this paper we extend our studies for Modified Lupas operators introduced by Sahai and Prasad. We introduce and develop some direct results for Stancu type generalization of above operators using linear approximation method. Fubini’s theorem is used extensively to prove our main theorem. The anticipated improvement is made through technique of linear combination is well corroborated by the results in the paper. Here, modification of operators through Stancu generalization plays an important role to obtain better approximation results.
Abstract: In this paper we extend our studies for Modified Lupas operators introduced by Sahai and Prasad. We introduce and develop some direct results for Stancu type generalization of above operators using linear approximation method. Fubini’s theorem is used extensively to prove our main theorem. The anticipated improvement is made through technique of li...
Show More
-

RBFs for Integral Equations with a Weakly Singular Kernel
Jafar Biazar,
Mohammad Ali Asadi
Issue:
Volume 3, Issue 6, December 2015
Pages:
250-255
Received:
29 September 2015
Accepted:
9 October 2015
Published:
21 October 2015
Abstract: In this paper a numerical method, based on collocation method and radial basis functions (RBF) is proposed for solving integral equations with a weakly singular kernel. Integrals appeared in the procedure of the solution are approximated by adaptive Lobatto quadrature rule. Illustrative examples are included to demonstrate the validity and applicability of the presented technique. In addition, the results of applying the method are compared with those of Homotopy perturbation, and Adomian decomposition methods.
Abstract: In this paper a numerical method, based on collocation method and radial basis functions (RBF) is proposed for solving integral equations with a weakly singular kernel. Integrals appeared in the procedure of the solution are approximated by adaptive Lobatto quadrature rule. Illustrative examples are included to demonstrate the validity and applicab...
Show More
-

Duplication of a Cube
Issue:
Volume 3, Issue 6, December 2015
Pages:
256-258
Received:
30 November 2014
Accepted:
3 April 2015
Published:
27 October 2015
Abstract: A cube is a hexahedron of six identical squares. Duplication of a cube; or the Delian Problem, means starting with a cube of edge e, having a volume if v3 then proceeding to replace it by another cube of edge k, having volume, 2e3. To construct the replacement cube requires the construction of k = e 3√2. Not until the 19thCentury was it proved that there was no possible geometric construction for k= e3√ 2. The solution to this problem is to bypass the impossible and deal with the possible by starting with a range of cubes of exactly known edges, en, and their corresponding exactly known volumes, Vn, and then establishing graphically the relationship between en and Vn, to produce a practical tool. Using this practical tool in conjunction with the well established problem solving technique of working backwards, any exact value of e and its corresponding value of volume V are determined by compass extent. A determination is made of the volume of the replacement cube- the duplication- by repeating in adjoining sequence, this compass extent twice on the volume axis. Identification of the corresponding value of edge e, on the graph gives the value of k, the edge of the replacement cube. With compass extent of value, k, the cube that duplicates the original is constructed.
Abstract: A cube is a hexahedron of six identical squares. Duplication of a cube; or the Delian Problem, means starting with a cube of edge e, having a volume if v3 then proceeding to replace it by another cube of edge k, having volume, 2e3. To construct the replacement cube requires the construction of k = e 3√2. Not until the 19thCentury was it proved that...
Show More
-

A New Fuzzy-Valued Additive Measure
Issue:
Volume 3, Issue 6, December 2015
Pages:
259-264
Received:
16 September 2015
Accepted:
9 October 2015
Published:
27 October 2015
Abstract: In this paper, we firstly invoke gradual Hausdorff metric to define a new additive fuzzy-valued measure on the ordinary measurable space. Then, from the view of a fuzzy number as a crisp interval of gradual numbers, we show that the new fuzzy-valued measure can be characterized by two gradual number-valued measures. Finally, we investigate some of its properties and structural characterizations.
Abstract: In this paper, we firstly invoke gradual Hausdorff metric to define a new additive fuzzy-valued measure on the ordinary measurable space. Then, from the view of a fuzzy number as a crisp interval of gradual numbers, we show that the new fuzzy-valued measure can be characterized by two gradual number-valued measures. Finally, we investigate some of ...
Show More
-

Krylov-Bogoliubov-Mitropolskii Method for Fourth Order More Critically Damped Nonlinear Systems
Issue:
Volume 3, Issue 6, December 2015
Pages:
265-270
Received:
15 September 2015
Accepted:
2 November 2015
Published:
17 November 2015
Abstract: With a view to obtaining the transient response of the system where triply eigenvalues are equal and another is distinct, we have considered a fourth order more critically damped nonlinear systems, and enquired into analytical approximate solution in this paper. We have also suggested that the results obtained by the proposed method correspond to the numerical solutions obtained by the fourth order Runge-Kutta method satisfactorily.
Abstract: With a view to obtaining the transient response of the system where triply eigenvalues are equal and another is distinct, we have considered a fourth order more critically damped nonlinear systems, and enquired into analytical approximate solution in this paper. We have also suggested that the results obtained by the proposed method correspond to t...
Show More
-

Modelling HIV/AIDS Transmission Dynamics Considering Counselling, Vaccination and Antiretroviral Therapy (ART) in a Population of Varying Size
Udoo Iorlumun Joseph Martins,
Kimbir Richard Anande,
Remilekun Mathew Odekunle
Issue:
Volume 3, Issue 6, December 2015
Pages:
271-282
Received:
6 October 2015
Accepted:
23 October 2015
Published:
24 November 2015
Abstract: A mathematical model of the transmission dynamics of HIV/AIDS, incorporating counselling, vaccination and antiretroviral therapy (ART) in a varying population, is presented. The existence and stability of the disease-free equilibrium states of the variants of the model are investigated, from which threshold values for vaccination and ART administration rates are established. Furthermore, numerical experiments are carried out to illustrate the effects of vaccination and ART, separately and in combination, on the transmission dynamics of HIV/AIDS in such populations.
Abstract: A mathematical model of the transmission dynamics of HIV/AIDS, incorporating counselling, vaccination and antiretroviral therapy (ART) in a varying population, is presented. The existence and stability of the disease-free equilibrium states of the variants of the model are investigated, from which threshold values for vaccination and ART administra...
Show More
-

Existence and Uniqueness of Weak Solution for Weighted p-bilaplacian (p-Biharmonic)
Bassam Al-Hamzah,
Naji Yebari
Issue:
Volume 3, Issue 6, December 2015
Pages:
283-287
Received:
27 September 2015
Accepted:
16 November 2015
Published:
9 December 2015
-

Analysis of MHD Mixed Convection Flow Within a Square Enclosure Containing a Triangular Obstacle
Kakali Chowdhury,
Md. Abdul Alim
Issue:
Volume 3, Issue 6, December 2015
Pages:
288-296
Received:
15 October 2015
Accepted:
29 October 2015
Published:
8 December 2015
Abstract: Finite element method is used to solve two-dimensional governing mass, momentum and energy equations for steady state, mixed convection problem inside a lid driven square enclosure containing a triangular hot obstacle located at the centre of the enclosure. The enclosure top wall is adiabatic while the bottom wall and triangular obstacle are maintained at a uniform temperature higher than the vertical side walls. The left vertical wall is moving with a uniform velocity by unity from bottom to top. All solid boundaries are in no slip condition. The aim of the study is to describe the effect of magnetic field, Prandtl number and the size of triangular obstacle on mixed convection fluid flow, heat transfer and temperature of the fluid. The investigation is conducted for various values of magnetic parameter Ha, obstacle size (area) A, Richardson number Ri, and Prandtl number Pr. Various results such as streamlines, isotherms, heat transfer rates in terms of average Nusselt number Nu, and average temperature θav of the fluid in the enclosure are presented for different parameters. It is observed that the obstacle size and dimensionless parameters Ha and Pr have significant effect on both the flow and thermal fields. The results also indicate that the average Nusselt number at the heated surface is strongly dependent on the configurations of the system studied under different geometrical and physical configurations.
Abstract: Finite element method is used to solve two-dimensional governing mass, momentum and energy equations for steady state, mixed convection problem inside a lid driven square enclosure containing a triangular hot obstacle located at the centre of the enclosure. The enclosure top wall is adiabatic while the bottom wall and triangular obstacle are mainta...
Show More
-

Numerical Solution of a Two Dimensional Poisson Equation with Dirichlet Boundary Conditions
Benyam Mebrate,
Purnachandra Rao Koya
Issue:
Volume 3, Issue 6, December 2015
Pages:
297-304
Received:
11 November 2015
Accepted:
22 November 2015
Published:
14 December 2015
Abstract: In this paper we have introduced Numerical techniques to solve a two dimensional Poisson equation together with Dirichlet boundary conditions. Specifically two methods are used for the purpose of numerical solution, viz. Finite difference method and Finite element method. The implementation of the solutions is done using Microsoft Office Excel worksheet or spreadsheet. The numerical solutions obtained by these two methods are also compared with each other graphically in two and three dimension.
Abstract: In this paper we have introduced Numerical techniques to solve a two dimensional Poisson equation together with Dirichlet boundary conditions. Specifically two methods are used for the purpose of numerical solution, viz. Finite difference method and Finite element method. The implementation of the solutions is done using Microsoft Office Excel work...
Show More
-

Numerical Solution of a One Dimensional Heat Equation with Dirichlet Boundary Conditions
Issue:
Volume 3, Issue 6, December 2015
Pages:
305-311
Received:
26 November 2015
Accepted:
4 December 2015
Published:
25 December 2015
Abstract: In this paper I present Numerical solutions of a one dimensional heat Equation together with initial condition and Dirichlet boundary conditions. Two methods are used to compute the numerical solutions, viz. Finite difference methods and Finite element methods. The finite element methods are implemented by Crank - Nicolson method. The numerical solutions of a one dimensional heat Equation together with initial condition and Dirichlet boundary conditions using finite difference methods do not always converge to the exact solutions. It indicates the occurrence of numerical instability in finite difference methods. Finally the numerical solutions obtained by these two methods are compared with the analytic solutions graphically into two and three dimensions.
Abstract: In this paper I present Numerical solutions of a one dimensional heat Equation together with initial condition and Dirichlet boundary conditions. Two methods are used to compute the numerical solutions, viz. Finite difference methods and Finite element methods. The finite element methods are implemented by Crank - Nicolson method. The numerical sol...
Show More
-

Enhancements of the Easter Algorithms (1940)
Charles Edward Ng’hwaya Masule
Issue:
Volume 3, Issue 6, December 2015
Pages:
312-320
Received:
17 August 2015
Accepted:
8 September 2015
Published:
25 December 2015
Abstract: Easter is a Christian yearly festival which falls on a Sunday of a full moon on the 22nd March at the least. One question that had remained unanswered for years however is: why Easter does not fall on due Sundays of a full moon at times? In this publication, a reasonable way had been developed on how to interface the much known Oudin’s Easter algorithm [1] to enable the pulling of the date of Easter one day back such that the occurrence of Easter on a full moon is possible. This will mean that: since the lunar month is 29.5 days long [3], the age of a full moon is 14.75 days and that: since the age of a full moon in the Easter algorithm is taken to be 15 days, it makes sense to pull the date of Easter a day back if the 15th day of a new moon falls on a Monday because – algorithmically - 6 hours of the full moon fall on the Sunday.
Abstract: Easter is a Christian yearly festival which falls on a Sunday of a full moon on the 22nd March at the least. One question that had remained unanswered for years however is: why Easter does not fall on due Sundays of a full moon at times? In this publication, a reasonable way had been developed on how to interface the much known Oudin’s Easter algor...
Show More
-

Heisenberg Form of Uncertainty Relations
Mohammed Yousif,
Mohammed Ali Basheir,
Emadaldeen Abdalrahim
Issue:
Volume 3, Issue 6, December 2015
Pages:
321-326
Received:
13 December 2015
Accepted:
21 December 2015
Published:
25 December 2015
Abstract: This paper, deals with the uncertainty relation for photons. In [Phys.Rev.Let.108, 140401 (2012)], and [1] the uncertainty relation was obtained as a sharp inequality by using the energy distribution on space. The relation we obtain here is an alternative to the one given in [Phys.Rev.Let.108, 140401 (2012)] by the use of the position of the center of the energy operator. The fact that the components of the center is non commutative affected the right hand side of the Heisenberg inequality. But this resolved by the increase of the photon energy. Furthermore we study the uncertainty of Heisenberg with respect to angular momentum and Foureir. We end the paper by giving some examples.
Abstract: This paper, deals with the uncertainty relation for photons. In [Phys.Rev.Let.108, 140401 (2012)], and [1] the uncertainty relation was obtained as a sharp inequality by using the energy distribution on space. The relation we obtain here is an alternative to the one given in [Phys.Rev.Let.108, 140401 (2012)] by the use of the position of the center...
Show More
-

Analysis of Prey – Predator System with Prey Population Experiencing Critical Depensation Growth Function
Mohammed Yiha Dawed,
Purnachandra Rao Koya,
Temesgen Tibebu
Issue:
Volume 3, Issue 6, December 2015
Pages:
327-334
Received:
30 November 2015
Accepted:
10 December 2015
Published:
30 December 2015
Abstract: In this paper we have presented a pair of coupled differential equations to represent a prey – predator system. It is assumed that the growth of the prey population follows critical depensation function and that of the predator population is negative in absence of the prey population. The critical depensation function is special since the growth rate is negative initially but positive later on. This function is stable both at the origin and at the carrying capacity while unstable at the critical mass quantity. The maximum and minimum rates of the critical depensation model are verified. It can be interpreted here that the prey represent fish and the predator represent a kind of birds that mostly feeding on fish to live. We showed the solution of the model is positive and bounded. The mathematical model of the system consisting of 7 parameters is constructed and shown that the non – dimensionalization decreases the number of model parameters to 4. The deterministic behavior of the model around feasible equilibrium points and criteria of the interior positive equilibrium points and their stability are explained. The trivial equilibrium point is always stable while the two axial equilibrium points and the lone interior equilibrium point are either stable or unstable depending on the conditions imposed on the parameters. The criterion for the existence of the limit cycle and the region of existence of interior equilibrium point are identified. Global stability of interior equilibrium points is also studied. For the interior equilibrium point of the model (i) the region of existence is identified (ii) Dulac’s criteria is applied to find the limit cycle and (iii) Lyaponov function is used to analyze the global stability. Simulation study of the model is conducted in support of the analytical analysis. To solidify the analytical results numerical simulations are provided for hypothetical set of parametric values.
Abstract: In this paper we have presented a pair of coupled differential equations to represent a prey – predator system. It is assumed that the growth of the prey population follows critical depensation function and that of the predator population is negative in absence of the prey population. The critical depensation function is special since the growth ra...
Show More
-

Modeling and Numerical Simulation of River Pollution Using Diffusion-Reaction Equation
Tsegaye Simon,
Purnachandra Rao Koya
Issue:
Volume 3, Issue 6, December 2015
Pages:
335-340
Received:
23 November 2015
Accepted:
6 December 2015
Published:
8 January 2016
Abstract: In the present study we have applied diffusion – reaction equation to describe the dynamics of river pollution and drawn numerical solution through simulation study. The diffusion-reaction equation is turn to be a partial differential equation since the independent variables are more than one that include spatial and temporal coordinates. The diffusion-reaction equation is widely applied to environmental studies in general and to river pollution studies in particular. River pollution models are special cases and are included in the broad area known as environmental studies. The diffusion – reaction equation is characterized by the reaction term. When the reaction term depends on the concentration of the contaminants then the original single diffusion-reaction equation will evolve to be a system of equations and this lead to analytical problems. The diffusion-reaction equations are difficult to solve analytically and hence we consider numerical solutions. For this purpose we first separate diffusion and reaction terms from the diffusion-reaction equation using splitting method and then apply numerical techniques such as Crank – Nicolson and Runge – Kutta of order four. These numerical methods are preferred because the systems of equations are solved accurately and efficiently. Detailed discussion of the results and their interpretations are included.
Abstract: In the present study we have applied diffusion – reaction equation to describe the dynamics of river pollution and drawn numerical solution through simulation study. The diffusion-reaction equation is turn to be a partial differential equation since the independent variables are more than one that include spatial and temporal coordinates. The diffu...
Show More
-

A Detailed Comparison Between Two Methods of Ranking Interval Efficiencies for Fuzzy DEA Models
Somayeh Tabatabaee,
Habib Hosseini
Issue:
Volume 3, Issue 6, December 2015
Pages:
341-344
Received:
22 November 2015
Accepted:
31 December 2015
Published:
23 February 2016
Abstract: Data envelopment analysis is a non-parametric technique for measuring and evaluating the relative efficiencies of a set of entities with common inputs and outputs. In fact, in a real evaluation problem input and output data of entities evaluated often fluctuate. This fluctuating data can be represented as linguistic variables characterized by fuzzy numbers for reflecting a kind of general feeling or experience of experts. For this purpose some researchers have proposed several models to deal with the efficiency evaluation problem with the given fuzzy input and output data. One of these methods is to change fuzzy models in to interval models by using alpha cuts. As we may face with some interval efficiency of several entities that should be compare with each other and ranked, in this paper we compare two methods of ranking interval efficiencies that is obtained from interval models. A sensitive difference between these two methods will be shown by a numerical example.
Abstract: Data envelopment analysis is a non-parametric technique for measuring and evaluating the relative efficiencies of a set of entities with common inputs and outputs. In fact, in a real evaluation problem input and output data of entities evaluated often fluctuate. This fluctuating data can be represented as linguistic variables characterized by fuzzy...
Show More