-

Reliability Systems and Optimal Control – Goal Realization Probability
Issue:
Volume 8, Issue 6, December 2020
Pages:
293-299
Received:
14 October 2020
Accepted:
29 October 2020
Published:
11 November 2020
Abstract: In this theoretical article is considered reliability cybernetics systems with probability theory. Optimal control and managing assigned goals of system are considered after control actions were assigned with a determined probability of realization. Real system is set of elements functionally connected in one whole for achieving determined goal using, transforming and exchanging energy, resources and informations. Real system mainly is presented as functional and physical whole. System researched by cybernetics could be school, metallic company or concrete factory. New concepts are involved in researching cybernetics systems reliability systems and optimal control. Controlling system is an action on object of control which optimized functioning of that object. Optimal control is substituted set of control actions which are got favorable optimal criterion value. Optimal criterions are considered as values of gains or value of losses. Reliability systems is property of system to realize his function or goal with some probability, having in mind reliability all of system elements. Realization wanted output or goal realization is calculated as intersection projected system parts realizations with determined probability. In this paper will be shown three different systems regarded to how they executed their controlling actions. Probability of realization system goals are calculated for two cases: maximum and minimum reliability. Intention is to show and calculate reliability systems with high human resources representation.
Abstract: In this theoretical article is considered reliability cybernetics systems with probability theory. Optimal control and managing assigned goals of system are considered after control actions were assigned with a determined probability of realization. Real system is set of elements functionally connected in one whole for achieving determined goal usi...
Show More
-

A Family of Global Attractors for the Higher-order Kirchhoff-type Equations and Its Dimension Estimation
Guoguang Lin,
Yuhang Chen
Issue:
Volume 8, Issue 6, December 2020
Pages:
300-310
Received:
4 November 2020
Accepted:
16 November 2020
Published:
24 November 2020
Abstract: In this paper, we study the long-time behavior of solutions for a class of initial boundary value problems of higher order Kirchhoff –type equations, and make appropriate assumptions about the Kirchhoff stress term. We use the uniform prior estimation and Galerkin method to prove the existence and uniqueness of the solution of the equation, when the order m and the order q meet certain conditions. Then, we use the prior estimation to get the bounded absorption set, it is further proved that using the Rellich-Kondrachov compact embedding theorem, the solution semigroup generated by the equation has a family of global attractor. Then the equation is linearized and rewritten into a first-order variational equation, and it is proved that the solution semigroup is Frechet differentiable. Finally, it proves that the Hausdorff dimension and Fractal dimension of a family of global attractors are finite.
Abstract: In this paper, we study the long-time behavior of solutions for a class of initial boundary value problems of higher order Kirchhoff –type equations, and make appropriate assumptions about the Kirchhoff stress term. We use the uniform prior estimation and Galerkin method to prove the existence and uniqueness of the solution of the equation, when th...
Show More
-

Continued Fraction Expansion of the Heinz Operator Mean
Kacem Belhroukia,
Salah Salhi,
Ali Kacha
Issue:
Volume 8, Issue 6, December 2020
Pages:
311-318
Received:
17 July 2020
Accepted:
9 September 2020
Published:
6 December 2020
Abstract: We recall that means arise in various contexts and contribute to solving many scientific problems. The aim of the present paper is to give a continued fraction expansion of the Heinz operator mean for two positive definite matrices. We note that the direct calculation of the Heinz operator mean proves difficult by the appearance of rational exponents of matrices. The main motivation of this work is to overcome these difficulties and to present a practical and efficient method for this calculation. We use the matrix continued fraction algorithm. At the end of our paper, we deduce a continued fraction representation of the symmetric operator entropy.
Abstract: We recall that means arise in various contexts and contribute to solving many scientific problems. The aim of the present paper is to give a continued fraction expansion of the Heinz operator mean for two positive definite matrices. We note that the direct calculation of the Heinz operator mean proves difficult by the appearance of rational exponen...
Show More
-

General Solutions of Some Complex Third-order Differential Equations
Issue:
Volume 8, Issue 6, December 2020
Pages:
319-326
Received:
10 November 2020
Accepted:
26 November 2020
Published:
8 December 2020
Abstract: According to the Nevanlinna theory, many researches have undertaken the behaviors of meromorphic solutions of complex ordinary differential equations (ODEs). Most of these researches have concentrated on the value distribution and growth of meromorphic solutions of ODEs. However, the existence of a meromorphic general solution is often used as a way to identify equations that are integrable. Especially, the existence of global meromorphic solutions of differential equation 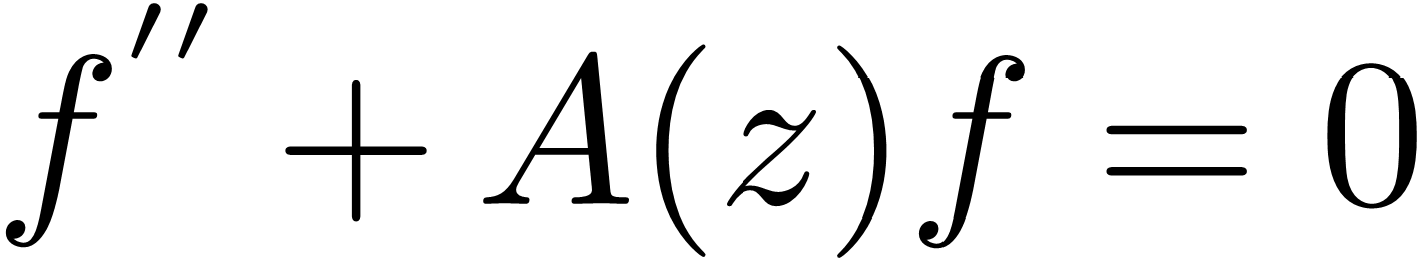 with entire coefficient can be settled, resulting in the characterization of Schwarzian derivatives. This is concerning with the linearly independent solutions of linear differential equations
with entire coefficient can be settled, resulting in the characterization of Schwarzian derivatives. This is concerning with the linearly independent solutions of linear differential equations  . The purpose of this present paper is to find explicit solutions of differential equation in terms of finite combinations of known functions, that is, we use local series methods and reduction of order to solve all linearly independent solutions of some third-order ODEs
. The purpose of this present paper is to find explicit solutions of differential equation in terms of finite combinations of known functions, that is, we use local series methods and reduction of order to solve all linearly independent solutions of some third-order ODEs 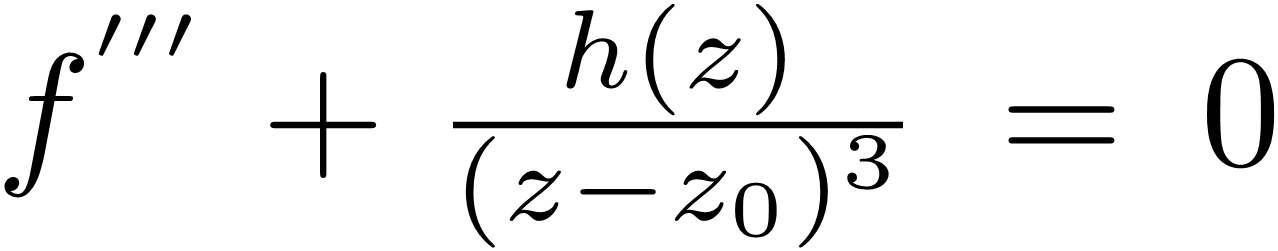 with entire coefficient
with entire coefficient 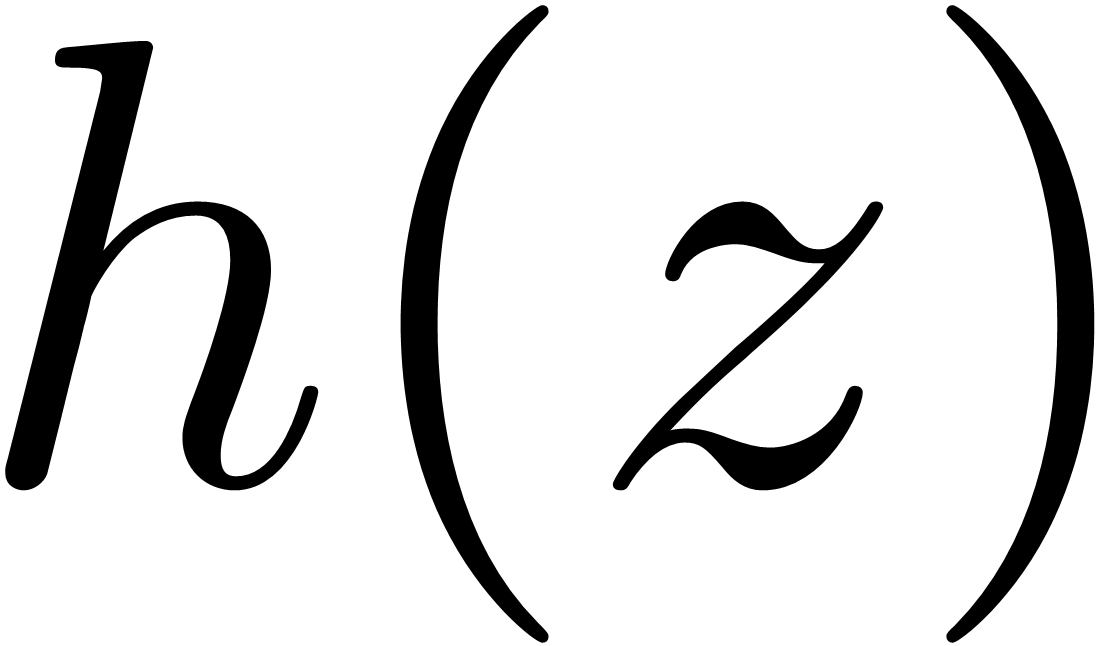 in the neighborhood of z0.
Abstract: According to the Nevanlinna theory, many researches have undertaken the behaviors of meromorphic solutions of complex ordinary differential equations (ODEs). Most of these researches have concentrated on the value distribution and growth of meromorphic solutions of ODEs. However, the existence of a meromorphic general solution is often used as a wa...
Show More
in the neighborhood of z0.
Abstract: According to the Nevanlinna theory, many researches have undertaken the behaviors of meromorphic solutions of complex ordinary differential equations (ODEs). Most of these researches have concentrated on the value distribution and growth of meromorphic solutions of ODEs. However, the existence of a meromorphic general solution is often used as a wa...
Show More
-

The Impulsive Motion of Flat Plate in Generalized Second Grade Fluid with Anomalous Diffusion
Mohammad Tanzil Hasan,
Md. Shafiqul Islam,
Mir Shariful Islam
Issue:
Volume 8, Issue 6, December 2020
Pages:
327-333
Received:
26 September 2020
Accepted:
3 November 2020
Published:
11 December 2020
Abstract: The flow adjacent to a wall rapidly set in motion for a generalized second-grade fluid with anomalous diffusion is examined. For the elucidation of such a fluid, the fractional-order derivative approach in the constitutive relationship model is presented because models based on ordinary differential equations have a relatively limited class of solutions, which does not provide compatible description of the complex systems in general. The current model of second-order fluid involving fractional calculus is based on the formal replacement of the first-order derivative in ordinary rheological constitutive equation by fractional derivative of a non-integer order. In addition, the time-fractional equation considered in this article describes the anomalous sub-diffusion. In this article, the velocity and stress field of generalized second-grade fluid with fractional anomalous diffusion are studied by fractional partial differential equations. Analytic solutions are given in closed form, from these differential equations in terms of the generalized G-functions or Fox's H-function with the discrete Laplace transform technique. Thus, many previous and classical results, namely, the solution of fractional diffusion equation obtained by Wyss, the classical Rayleigh’s time-space regularity solution, the relationship between velocity field and stress field obtained by Bagley and Torvik, are represented by particular cases of our proposed derivation.
Abstract: The flow adjacent to a wall rapidly set in motion for a generalized second-grade fluid with anomalous diffusion is examined. For the elucidation of such a fluid, the fractional-order derivative approach in the constitutive relationship model is presented because models based on ordinary differential equations have a relatively limited class of solu...
Show More
-

Solving Highly Nonlinear Partial Differential Equations Using Homotopy Perturbation Method
Amanat Ali Khan,
Musammet Tahmina Akter
Issue:
Volume 8, Issue 6, December 2020
Pages:
334-343
Received:
12 November 2020
Accepted:
26 November 2020
Published:
11 December 2020
Abstract: An elegant and powerful technique is Homotopy Perturbation Method (HPM) to solve linear and nonlinear ordinary and partial differential equations. The method, which is a coupling of the traditional perturbation method and homotopy in topology, deforms continuously to a simple problem which can be solved easily. The method does not depend upon a small parameter in the equation. Using the initial conditions this method provides an analytical or exact solution. From the calculation and its graphical representation it is clear that how the solution of the original equation and its behavior depends on the initial conditions. Therefore there have been attempts to develop new techniques for obtaining analytical solutions which reasonably approximate the exact solutions. Many problems in natural and engineering sciences are modeled by nonlinear partial differential equations (NPDEs). The theory of nonlinear problem has recently undergone much study. Nonlinear phenomena have important applications in applied mathematics, physics, and issues related to engineering. In this paper we have applied this method to Burger’s equation and an example of highly nonlinear partial differential equation to get the most accurate solutions. The final results tell us that the proposed method is more efficient and easier to handle when is compared with the exact solutions or Adomian Decomposition Method (ADM).
Abstract: An elegant and powerful technique is Homotopy Perturbation Method (HPM) to solve linear and nonlinear ordinary and partial differential equations. The method, which is a coupling of the traditional perturbation method and homotopy in topology, deforms continuously to a simple problem which can be solved easily. The method does not depend upon a sma...
Show More
-

Modelling Covid-19 Deaths in Ghana as a Discrete State Process in Continuous Time
Osei Antwi,
Abdul Martinu Issah
Issue:
Volume 8, Issue 6, December 2020
Pages:
344-355
Received:
30 November 2020
Accepted:
18 December 2020
Published:
31 December 2020
Abstract: We propose a stochastic process modelling of covid-19 deaths in Ghana. The objective is to accurately capture the death processes resulting from the pandemic and to predict future deaths resulting from Covid-19 infections in Ghana. The mathematical derivation is based strictly on the compound Poisson process, a class of a Levy process. The model is verified by using empirical data of deaths resulting from Covid-19 from the onset of the pandemic up to the time of writing this report. That is, Covid-19 deaths in Ghana from March to August 2020. The method departs slightly from the usual differential equations used in modeling pandemics due to the unique occurrence of deaths from the disease in Ghana. As the methods are basically compound Poisson process, we delve into Levy processes as it allows us to effectively simulate the future behaviour of the death process. To test the effectiveness of the model, we compared the simulated results to the actual reported number of deaths from Covid-19 cases in Ghana from March to August 2020. The results show that at a 95% confidence interval there is no significant difference between the actual deaths and the simulated results. The results of the simulation, when extended to February 2021 (one year after the advent of the pandemic) shows that if the current conditions remain same, that is, if there is no immediate intervention by the discovery of an effective drug or a vaccine, then the number of deaths could reach four hundred and forty six (446) by February 28, 2020.We propose a stochastic process modelling of covid-19 deaths in Ghana. The objective is to accurately capture the death processes resulting from the pandemic and to predict future deaths resulting from Covid-19 infections in Ghana. The mathematical derivation is based strictly on the compound Poisson process, a class of a Levy process. The model is verified by using empirical data of deaths resulting from Covid-19 from the onset of the pandemic up to the time of writing this report. That is, Covid-19 deaths in Ghana from March to August 2020. The method departs slightly from the usual differential equations used in modeling pandemics due to the unique occurrence of deaths from the disease in Ghana. As the methods are basically compound Poisson process, we delve into Levy processes as it allows us to effectively simulate the future behaviour of the death process. To test the effectiveness of the model, we compared the simulated results to the actual reported number of deaths from Covid-19 cases in Ghana from March to August 2020. The results show that at a 95% confidence interval there is no significant difference between the actual deaths and the simulated results. The results of the simulation, when extended to February 2021 (one year after the advent of the pandemic) shows that if the current conditions remain same, that is, if there is no immediate intervention by the discovery of an effective drug or a vaccine, then the number of deaths could reach four hundred and forty six (446) by February 28, 2020.
Abstract: We propose a stochastic process modelling of covid-19 deaths in Ghana. The objective is to accurately capture the death processes resulting from the pandemic and to predict future deaths resulting from Covid-19 infections in Ghana. The mathematical derivation is based strictly on the compound Poisson process, a class of a Levy process. The model is...
Show More






