-

Ambiguity—Risk—Return: Evidence from the Stock Market in China
Yingxiu Zhao,
Baojuan Shi,
Fang Song,
Lin Zhou
Issue:
Volume 10, Issue 4, August 2022
Pages:
118-124
Received:
25 May 2022
Accepted:
27 June 2022
Published:
5 July 2022
DOI:
10.11648/j.ajam.20221004.11
Downloads:
Views:
Abstract: In the past decades, ambiguity in the stock market has been widely studied theoretically and experimentally. Most existing studies focus on foreign financial markets, such as American stock market. However, there are essential differences between Chinese stock market and others stock market, such as its participants and trading mechanisms. Therefore, it is necessary to study the relation of ambiguity, risk and expected return in China's stock market. This study analyzes CSI 300 index data for January 2006 to February 2020 to investigate the relationships between ambiguity, risk, and expected returns in China’s stock market. We apply empirical methods to measure the degree of ambiguity and assess attitudes toward ambiguity from the China's market data, the results indicate that: (1) the degree of ambiguity increases with the expected return; (2) when risk and ambiguity are introduced simultaneously, the expected return of China's stock market is significant negative; and (3) in addition, we also prove that the investors’ level of aversion to or preference for ambiguity, which depends on the expected probability of favorable returns. In sum, our results not only clarify ambiguity and risk regarding expected returns but also provide the theoretical and practical implications for the problem of asset prices in China's stock market.
Abstract: In the past decades, ambiguity in the stock market has been widely studied theoretically and experimentally. Most existing studies focus on foreign financial markets, such as American stock market. However, there are essential differences between Chinese stock market and others stock market, such as its participants and trading mechanisms. Therefor...
Show More
-

Existence and Multiplicity of Solutions for a Class of Quasilinear Schrödinger Equations ♦
Issue:
Volume 10, Issue 4, August 2022
Pages:
125-133
Received:
22 June 2022
Accepted:
8 July 2022
Published:
26 July 2022
DOI:
10.11648/j.ajam.20221004.12
Downloads:
Views:
Abstract: Quasilinear Schrödinger equations appear in several differential physical phenomena. We consider the quasilinear Schrödinger equation
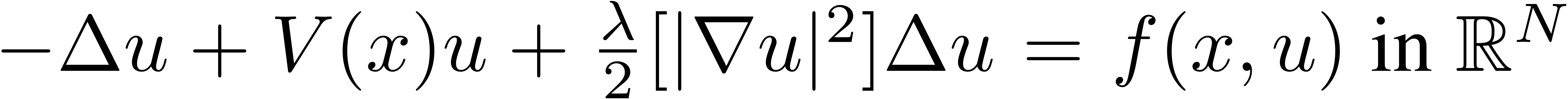
, where
V and
f are periodic in
x1,...,xN and
f is odd in
u and subcritical. By employing the genus theory and variational method, we only need
f is continuous, which is allowed to have weaker asymptotic growth than usually assumed, and obtain infinitely many geometrically distinct solutions for
λ > 0.
-

Decompositions of the Covariance Matrix of the Discrete Brownian Bridge: New Fast Constructions of Discrete Brownian Motions and Brownian Bridges
Sung-hyon Ri,
Ye-rim Ki,
Kwang Ri
Issue:
Volume 10, Issue 4, August 2022
Pages:
134-140
Received:
20 June 2022
Accepted:
19 July 2022
Published:
17 August 2022
DOI:
10.11648/j.ajam.20221004.13
Downloads:
Views:
Abstract: Fast constructions from the Brownian motion and Brownian bridge are required in many applications such as Quasi-Monte Carlo simulations and statistical inferences on stochastic processes. The simple method for construction of discrete Brownian motion is a step-by-step method of computing the cumulative sum of i.i.d. normal variables. The construction of a N dimensional discrete Brownian motion (or a N-1 dimensional discrete Brownian bridge) that require at most O(NlogN) floating point operations(flops) is called fast one. Discrete Brownian motion can be also constructed using decompositions of its covariance matrix and the method based on eigenvalue decomposition not only shows superior performances in many simulations to the step-by-step method but also becomes a fast construction. Usually the discrete Brownian bridge can be constructed from the discrete Brownian motion using the linear relationship between them. In this paper, the inverse of the covariance matrix for the discrete Brownian bridge is computed. The explicit expression of eigenvalue decomposition for the covariance matrix is given. Using it, a fast construction of the discrete Brownian Bridge is derived. The LDU (Lower-Diagonal-Upper) decompositions of the covariance matrices for the discrete Brownian motion and Brownian Bridge are obtained, respectively. The constructions of the discrete Brownian motion and Brownian bridge derived from these decompositions are fast ones and have step-by-step types. It is interesting that the discrete Brownian bridge is constructed as the cumulative sum of normal variables. Performances of the step-by-step method and methods using LDU and eigenvalue decompositions are compared through simulation results on the maximum distributions of the Brownian motion and Brownian bridge. Finally, an inserting method for construction of discrete Brownian motion using eigenvalue decompositions which requires O(Nlog(logN)) flops is proposed. The new fast constructions could be significant in Quasi-Monte Carlo simulations require high accuracy.
Abstract: Fast constructions from the Brownian motion and Brownian bridge are required in many applications such as Quasi-Monte Carlo simulations and statistical inferences on stochastic processes. The simple method for construction of discrete Brownian motion is a step-by-step method of computing the cumulative sum of i.i.d. normal variables. The constructi...
Show More
-

Axisymmetric Problem of Stationnary Navier-Stokes Equations Coupled with the Heat Equation
Rachid Ghenji,
Mohamed El Hatri
Issue:
Volume 10, Issue 4, August 2022
Pages:
141-159
Received:
26 June 2022
Accepted:
26 July 2022
Published:
17 August 2022
DOI:
10.11648/j.ajam.20221004.14
Downloads:
Views:
Abstract: In this work, we are interested in the mathematical study of the flow of a Newtonian Navier-Stokes fluid, coupled to the energy equation, in a domain with axial symmetry. The study consists first of all in reducing this problem, which is posed in a domain in dimension three (3-D), to a problem whose spatial domain is in dimension two, using the transformation of Cartesian coordinates in cylindrical coordinates, assuming that the problem data does not depend on the angle of rotation. The problem thus obtained is a so-called axially symmetric problem presenting a degeneracy on the axis of symmetry, hence the interest of this study. The study of this problem is the subject of the first part of this article which deals with the existence and uniqueness of the weak solution of the problem in a Sobolev space with appropriate weight. The results of this part have already been published by the same authors that we recall here with some slight modifications in order to facilitate the reading and understanding of the second part of the article. In this second part, we approach the existence and the unicity of the numerical solution of the posed problem. It is obtained using the Lagrange finite element method whose polinomial space is of degree one. The study in question highlights the necessary algebraic relations between the different physical parameters of the problem to which the flow in question obeys.
Abstract: In this work, we are interested in the mathematical study of the flow of a Newtonian Navier-Stokes fluid, coupled to the energy equation, in a domain with axial symmetry. The study consists first of all in reducing this problem, which is posed in a domain in dimension three (3-D), to a problem whose spatial domain is in dimension two, using the tra...
Show More
-

Algebraic Points of Degree at Most 3 on the Affine Equation Curve y11=x4(x-1)4
Mouhamadou Diaby Gassama,
Oumar Sall
Issue:
Volume 10, Issue 4, August 2022
Pages:
160-175
Received:
29 May 2022
Accepted:
13 July 2022
Published:
18 August 2022
DOI:
10.11648/j.ajam.20221004.15
Downloads:
Views:
Abstract: The quotients of Fermat curves Cr,s(p) are studied by Oumar SALL. Among these studies are the cases Cr,s(11) for r = s = 1. Mamina COLY and Oumar SALL have explicitly determined the algebraic points of degree at most 3 on Q for the cases Cr,s(11) for r = s = 2. Our work focuses on determining explicitly the algebraic points of degree at most 3 on Q on the curve C4,4(11) which is a special case of Fermat quotient curves. Our study concerns the cases Cr,s(11) for r = s = 4. It seems that the finiteness of the Mordell-Weil group of rational points of the Jacobien J4,4(11)(Q) is an essential condition. So to determine the algebraic points on the curve C4,4(11) we need a finiteness of the Mordeill-Weill group of rational points of the Jacobien J4,4(11)(Q). The Mordell-Weil group J4,4(11)(Q) of rational points of the Jacobien is finite according to Faddev. Our note is in this framework. Our essential tools in this note are the Mordell-Weil group J4,4(11)(Q) of the Jacobien of C4,4(11) the Abel-Jacobi theorem and the study of linear systems on the curve C4,4(11). The result obtained concerns some quotients of Fermat curves. Indeed, the curve C4,4(11) which is the subject of our study, the set of algebraic points of degree at most 3 on Q has been determined in an explicit way, to achieve this we have determined the quadratic points on the curve C4,4(11) on Q and the cubic points on the curve C4,4(11) on Q.
Abstract: The quotients of Fermat curves Cr,s(p) are studied by Oumar SALL. Among these studies are the cases Cr,s(11) for r = s = 1. Mamina COLY and Oumar SALL have explicitly determined the algebraic points of degree at most 3 on Q for the cases Cr,s(11) for r = s = 2. Our work focuses on determining explicitly the algebraic points of degree at most 3 on Q...
Show More




